题目内容
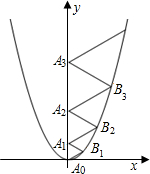 二次函数y=
二次函数y=| 2 |
| 3 |
| 2 |
| 3 |
考点:二次函数图象上点的坐标特征,等边三角形的性质
专题:规律型
分析:设△A0B1A1的边长为a,根据等边三角形的性质表示出点B1的坐标,然后代入二次函数解析式解方程即可得到a的值,同理求出△A1B2A2的边长b,△A2B3A3的边长c,…,不难发现,等边三角形的边长等于它相应的序数,然后写出即可.
解答:解:设第一个等边三角形的边长为a,
∵△A0B1A1是等边三角形,
∴点B1的横坐标为
a,纵坐标为
a,
∴B1(
a,
a),
∵B1在二次函数y=
x2位于第一象限的图象上,
∴
×(
a)2=
a,
解得a=1,
∴△A0B1A1的边长为1,
同理,设△A1B2A2的边长为b,
则B2(
b,
b+1),
代入二次函数解析式得,
×(
b)2=
b+1,
解得b=2,b=-1(舍去),
所以,△A1B2A2的边长为2,
设△A2B3A3的边长c,则B3(
c,
c+1+2),
代入二次函数解析式得,
×(
c)2=
c+1+2,
解得c=3,c=-2(舍去),
所以,△A2B3A3的边长为3,
…,
以此类推,等边三角形的边长等于它相应的序数,
所以,△A2013B2014A2014的边长=2014.
故答案为:2014.
∵△A0B1A1是等边三角形,
∴点B1的横坐标为
| ||
| 2 |
| 1 |
| 2 |
∴B1(
| ||
| 2 |
| 1 |
| 2 |
∵B1在二次函数y=
| 2 |
| 3 |
∴
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
解得a=1,
∴△A0B1A1的边长为1,
同理,设△A1B2A2的边长为b,
则B2(
| ||
| 2 |
| 1 |
| 2 |
代入二次函数解析式得,
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
解得b=2,b=-1(舍去),
所以,△A1B2A2的边长为2,
设△A2B3A3的边长c,则B3(
| ||
| 2 |
| 1 |
| 2 |
代入二次函数解析式得,
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
解得c=3,c=-2(舍去),
所以,△A2B3A3的边长为3,
…,
以此类推,等边三角形的边长等于它相应的序数,
所以,△A2013B2014A2014的边长=2014.
故答案为:2014.
点评:本题考查了二次函数图象上点的坐标特征,等边三角形的性质,根据等边三角形的性质表示出点B系列的坐标是解题的关键,也是本题的难点.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
若等腰三角形有两条边的长度为2和5,则此等腰三角形的周长为( )
| A、9 | B、12 | C、9或12 | D、10 |
 如图,AB是⊙O的直径,D是⊙O上一点,过点D作⊙0的切线交AB的延长线于点C,若∠C=20°,则∠A等于( )
如图,AB是⊙O的直径,D是⊙O上一点,过点D作⊙0的切线交AB的延长线于点C,若∠C=20°,则∠A等于( )| A、70° | B、50° |
| C、40° | D、35° |
 如图,在边长为9的正方形ABCD中,F为AB上一点,连接CF.过点F作FE⊥CF,交AD于点E,若AF=3,则AE等于
如图,在边长为9的正方形ABCD中,F为AB上一点,连接CF.过点F作FE⊥CF,交AD于点E,若AF=3,则AE等于