Question

【题目】在数学活动课上，老师要求学生在5×5的正方形ABCD网格中（小正方形的边长为1）画等腰三角形，要求三个顶点都在格点上（小正方形的顶点称为格点），用实线画四种图形，且分别符合下列各条件：

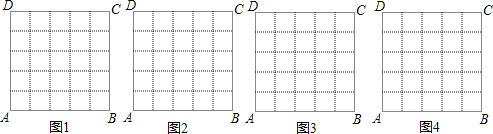
（1）面积为2（画在图1中）；

（2）面积为4，且三边与AB或AD都不平行（画在图2中）；

（3）面积为5，且三边与AB或AD都不平行（画在图3中）；

（4）面积为，且三边与AB或AD都不平行（画在图4中）．

Answer 1

【答案】（1）见解析；（2）见解析；（3）见解析；（4）见解析

【解析】

（1）利用等腰三角形的对称性，计算等腰三角形的面积可求图形；

（2）利用等腰三角形的对称性，计算等腰三角形的面积可求图形；

（3）利用等腰三角形的对称性，计算等腰三角形的面积可求图形；

（4）利用等腰三角形的对称性，计算等腰三角形的面积可求图形．

解：（1）如图1

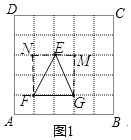
∵ME＝EN，MG＝FN，∠EMG＝∠FNE＝90°

∴△EMG≌△EFN

∴EG＝EF

∴△EFG是等腰三角形

∵S△EFG＝×2×2＝2

∴△EFG为所求等腰三角形．

（2）如图2

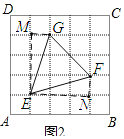
∵ME＝EN，MG＝FN，∠EMG＝∠FNE＝90°

∴△EMG≌△EFN

∴EG＝EF

∴△EFG是等腰三角形

∵S△EFG＝3×3﹣2×＝4

∴△EFG为所求等腰三角形．

（3）如图3

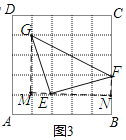
∵ME＝EN，MG＝FN，∠EMG＝∠FNE＝90°

∴△EMG≌△EFN

∴EG＝EF

∴△EFG是等腰三角形

∵S△EFG＝3×4﹣2×＝5

∴△EFG为所求三角形．

（4）如图4

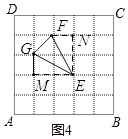
∵ME＝EN，MG＝FN，∠EMG＝∠FNE＝90°

∴△EMG≌△EFN

∴EG＝EF

∴△EFG是等腰三角形

∵S△EFG＝2×2﹣2××2×1﹣×1×1＝

∴△EFG为所求等腰三角形