题目内容
14.已知命题“关于x的一元二次方程2x2+bx+2=0,当b<0时必有实数解”,能说明这个命题是假命题的一个反例可以是( )| A. | b=-1 | B. | b=1 | C. | b=-4 | D. | b=5 |
分析 先计算出判别式得到△=b2-16,要举一个反例,则b满足b<0且方程没有实数解,然后对四个选项进行判断.
解答 解:△=b2-4×2×2=b2-16,
当b=-1时,△=1-16<0,此时方程没有实数解,
所以能说明命题“关于x的一元二次方程2x2+bx+2=0,当b<0时必有实数解”是假命题的一个反例可以为b=-1.
故选A.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 有些命题的正确性是用推理证实的,这样的真命题叫做定理. 任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.下列计算中,正确的是( )
| A. | $\sqrt{9}$=±3 | B. | (-$\frac{1}{3}$)-1=-3 | C. | 2a+3b=5ab | D. | a6÷a2=a3 |
2.下列命题错误的是( )
| A. | 对角线相互平分的四边形是平行四边形 | |
| B. | 对角线相互平分且相等的四边形是矩形 | |
| C. | 对角线相互平分且垂直的四边形是菱形 | |
| D. | 对角线相等且垂直的四边形是正方形 |
9.下列各运算中,计算正确的是( )
| A. | 3x2+5x2=8x4 | B. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | ||
| C. | $\frac{1}{x+1}$-$\frac{1}{x-1}$=$\frac{2}{{{x^2}-1}}$ | D. | (-$\frac{1}{2}$m2n)2=$\frac{1}{4}$m4n2 |
19.在直角坐标系中,点P落在直线x-2y+6=0上,O为坐标原点,则|OP|的最小值为( )
| A. | $\frac{{3\sqrt{5}}}{2}$ | B. | $3\sqrt{5}$ | C. | $\frac{{6\sqrt{5}}}{5}$ | D. | $\sqrt{10}$ |
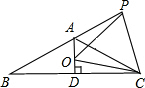 已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,
已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,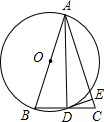 (1)如图,在△ABC中,以AB为直径的⊙O交BC于点D,连接AD,请你添加一个条件,使△ABD≌△ACD,并说明全等的理由,你添加的条件是:BD=DC.
(1)如图,在△ABC中,以AB为直径的⊙O交BC于点D,连接AD,请你添加一个条件,使△ABD≌△ACD,并说明全等的理由,你添加的条件是:BD=DC.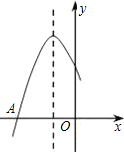 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是①④.
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是①④.