题目内容
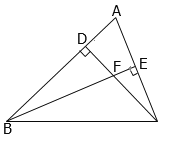
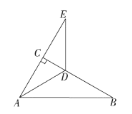
【题目】如图,在Rt△ABC中,∠A=90°,AB=12,AC=16,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.
(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)若线段PQ与线段DE的交点为F,当△PDF为等腰三角形时,求BP的长.
【答案】(1)DE=![]() ,CE=
,CE=![]() ;(2)CQ的长为11或14;(3)BP=
;(2)CQ的长为11或14;(3)BP=![]() 或
或![]() .
.
【解析】(1)先根据勾股定理求得BC的长,再结合点D为BC的中点可得CD的长,然后证得△ABC∽△DEC,根据相似三角形的性质即可求得结果;(2)分点P在AB边上和点P在AB的延长线上两种情况求解即可;(3)先证得△PDF∽△CDQ,因△PDF为等腰三角形 可得△CDQ为等腰三角形,再分CQ=CD、QC=QD和DC=DQ三种情况,根据等腰三角形的性质求解即可.
(1)∵∠A=90°,AB=12,AC=16,
∴根据勾股定理得到,BC=![]() =20,
=20,
∴CD=![]() BC=10,
BC=10,
∵DE⊥BC,
∴∠A=∠CDE=90°,∠C=∠C,
∴△CDE∽△CAB,
∴DE:AB=CE:CB=CD:CA,
即DE:12=CE:20=10:16,
∴DE=![]() ,CE=
,CE=![]() ;
;
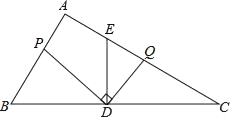
(2)分两种情况考虑:
如图,∵△CDE∽△CAB,
∴∠B=∠DEC,
∵∠PDQ=90°,
∴∠QDC+∠PDB=90°,
∵∠QDC+∠EDQ=90°,
∴∠EDQ=∠PDB,
∴△PBD∽△QED,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴EQ=![]() ,
,
∴CQ=CE﹣EQ=![]() ﹣
﹣![]() =11;
=11;
如图2,
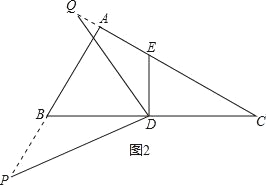
∵∠B=DEC,
∴∠PBD=∠QED,
∵∠PDQ=90°
∴∠BPD+∠QDB=90°,
∵∠QDE+∠QDB=90°,
∴∠BDP=∠QDE,
∴△PBD∽△QED,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴EQ=![]() ,
,
∴CQ=![]() +
+![]() =14,
=14,
则CQ的长为11或14;
(3)∵线段PQ与线段DE的交点为点FF,
∴点P在边AB上,
∵△BPD∽△EQD,
∴![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
若设BP=x,则EQ=![]() x,CQ=
x,CQ=![]() ﹣
﹣![]() x,
x,
∵cot∠QPD=![]() =
=![]() ,cotC=
,cotC=![]() =
=![]() =
=![]() ,
,
∴∠QPD=∠C,
∵∠PDE=∠CDQ,∴△PDF∽△CDQ,
∵△PDF为等腰三角形,
∴△CDQ为等腰三角形,
①当CQ=CD时,可得:![]() ﹣
﹣![]() x=10,
x=10,
解得:x=![]() ;
;
②当QC=QD时,过点Q作QM⊥CB于M,如图3所示,

∴CM=![]() CD=5,
CD=5,
∵cos∠C=![]() =
=![]() =
=![]() =
=![]() ,
,
∴CQ=![]() ,
,
∴![]() ﹣
﹣![]() x=
x=![]() ,
,
解得:x=![]() ;
;
③当DC=DQ时,过点D作DN⊥CQ于N,如图4所示,
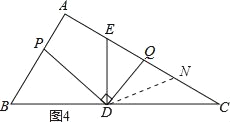
∴CQ=2CN,
∵cos∠C=![]() =
=![]() =
=![]() ,
,
∴CN=8,
∴CQ=16,
∴![]() ﹣
﹣![]() x=16,
x=16,
解得:x=﹣![]() (舍去),
(舍去),
∴综上所述,BP=![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案