ЬтФПФкШн
ЁОЬтФПЁПдФЖСРэНтЃК
Шє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЪ§жсЩЯШ§ЕуЧвЕу
ЮЊЪ§жсЩЯШ§ЕуЧвЕу![]() дк
дк![]() ЃЌ
ЃЌ![]() жЎМфЃЌШєЕу
жЎМфЃЌШєЕу![]() ЕН
ЕН![]() ЕФОрРыЪЧЕу
ЕФОрРыЪЧЕу![]() ЕН
ЕН![]() ЕФОрРыЕФ3БЖЃЌЮвУЧОЭГЦЕу
ЕФОрРыЕФ3БЖЃЌЮвУЧОЭГЦЕу![]() ЪЧ
ЪЧ![]() ЕФКУЕуЃЎ
ЕФКУЕуЃЎ
ШчЭМ1ЃЌЕу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ЃЌЕу
ЃЌЕу![]() БэЪОЕФЪ§ЮЊ2ЃЎБэЪО1ЕФЕу
БэЪОЕФЪ§ЮЊ2ЃЎБэЪО1ЕФЕу![]() ЕН
ЕН![]() ЕФОрРыЪЧ3ЃЌЕН
ЕФОрРыЪЧ3ЃЌЕН![]() ЕФОрРыЪЧ1ЃЌФЧУДЕу
ЕФОрРыЪЧ1ЃЌФЧУДЕу![]() ЪЧ
ЪЧ![]() ЕФКУЕуЃЛгжШчЃЌБэЪО
ЕФКУЕуЃЛгжШчЃЌБэЪО![]() ЕФЕу
ЕФЕу![]() ЕН
ЕН![]() ЕФОрРыЪЧ1ЃЌЕН
ЕФОрРыЪЧ1ЃЌЕН![]() ЕФОрРыЪЧ3ЃЌФЧУДЕу
ЕФОрРыЪЧ3ЃЌФЧУДЕу![]() ОЭВЛЪЧ
ОЭВЛЪЧ![]() ЕФКУЕуЃЌЕЋЕу
ЕФКУЕуЃЌЕЋЕу![]() ЪЧ
ЪЧ![]() ЕФКУЕуЃЎ
ЕФКУЕуЃЎ
жЊЪЖдЫгУЃК
ЃЈ1ЃЉШє![]() ЁЂ
ЁЂ![]() ЮЊЪ§жсЩЯСНЕуЃЌЕу
ЮЊЪ§жсЩЯСНЕуЃЌЕу![]() ЫљБэЪОЕФЪ§ЮЊ
ЫљБэЪОЕФЪ§ЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЫљБэЪОЕФЪ§ЮЊ2ЃЎ
ЫљБэЪОЕФЪ§ЮЊ2ЃЎ
Ъ§ ЫљБэЪОЕФЕуЪЧ![]() ЕФКУЕуЃЛ
ЕФКУЕуЃЛ
Ъ§ ЫљБэЪОЕФЕуЪЧ![]() ЕФКУЕуЃЛ
ЕФКУЕуЃЛ
ЃЈ2ЃЉШєЕу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ЃЌЕу
ЃЌЕу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ЃЌЕу
ЃЌЕу![]() дкЕу
дкЕу![]() ЕФгвБпЃЌЧвЕу
ЕФгвБпЃЌЧвЕу![]() дк
дк![]() ЃЌ
ЃЌ![]() жЎМфЃЌЕу
жЎМфЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФКУЕуЃЌЧѓЕу
ЕФКУЕуЃЌЧѓЕу![]() ЫљБэЪОЕФЪ§ЃЈгУКЌ
ЫљБэЪОЕФЪ§ЃЈгУКЌ![]() ЁЂ
ЁЂ![]() ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ3ЃЉШє![]() ЁЂ
ЁЂ![]() ЮЊЪ§жсЩЯСНЕуЃЌЕу
ЮЊЪ§жсЩЯСНЕуЃЌЕу![]() ЫљБэЪОЕФЪ§ЮЊ
ЫљБэЪОЕФЪ§ЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЫљБэЪОЕФЪ§ЮЊ27ЃЌЯжгавЛжЛЕчзгТьвЯ
ЫљБэЪОЕФЪ§ЮЊ27ЃЌЯжгавЛжЛЕчзгТьвЯ![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвдУПУы6ИіЕЅЮЛЕФЫйЖШЯђгвдЫЖЏЃЌдЫЖЏЪБМфЮЊ
ГіЗЂЃЌвдУПУы6ИіЕЅЮЛЕФЫйЖШЯђгвдЫЖЏЃЌдЫЖЏЪБМфЮЊ![]() УыЃЎШчЙћ
УыЃЎШчЙћ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жаЧЁгавЛИіЕуЮЊЦфгрСНЕуЕФКУЕуЃЌЧѓ
жаЧЁгавЛИіЕуЮЊЦфгрСНЕуЕФКУЕуЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ


ЁОД№АИЁПЃЈ1ЃЉ0ЃЌ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ40ЃЎ
ЁЂ40ЃЎ
ЁОНтЮіЁП
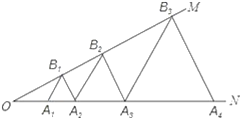
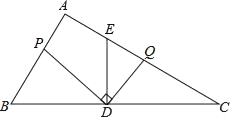
ЃЈ1ЃЉИљОнЬтвтжЊЃЌЫљЧѓЕФКУЕуЪЧЯпЖЮMNЕФ4ЕШЗжЕуЃЛ
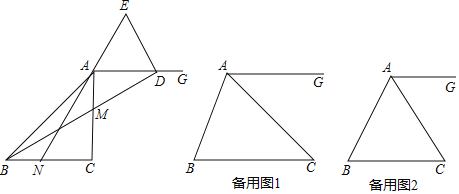
ЃЈ2ЃЉгЩгкЕуBЪЧЁОCЃЌAЁПЕФКУЕуЃЌЫљвдBC=3BAЃЌОнДЫЕуCЫљБэЪОЕФЪ§ЃЈгУКЌaЁЂbЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ3ЃЉашвЊЗжРрЬжТлЃКЂйPЪЧЁОAЃЌBЁПЕФКУЕуЃЌЂкPЪЧЁОBЃЌAЁПЕФКУЕуЃЌЂлBЪЧЁОAЃЌPЁПЕФКУЕуЃЌЂмBЪЧЁОPЃЌAЁПЕФКУЕуЃЌИљОнЁАКУЕуЁБЕФЖЈвхСаГіЯргІЕФЗНГЬВЂНтД№ЃЎ
ЃЈ1ЃЉгЩЬтвтжЊЃЌЪ§0ЫљБэЪОЕФЕуЪЧ![]() ЕФКУЕуЃЛ
ЕФКУЕуЃЛ
Ъ§![]() ЫљБэЪОЕФЕуЪЧ
ЫљБэЪОЕФЕуЪЧ![]() ЕФКУЕуЃЛ
ЕФКУЕуЃЛ
ЙЪД№АИЪЧЃК0ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшЕу![]() ЫљБэЪОЕФЪ§ЮЊ
ЫљБэЪОЕФЪ§ЮЊ![]() ЃЌ
ЃЌ
вРЬтвтЕУ
![]()
![]()
![]()
ЃЈ3ЃЉвРЬтвтЕУЃЌ![]()
Ђй![]() ЪЧ
ЪЧ![]() ЕФКУЕу
ЕФКУЕу
![]()
![]()
![]()
Ђк![]() ЪЧ
ЪЧ![]() ЕФКУЕу
ЕФКУЕу
![]()
![]()
![]()
Ђл![]() ЪЧ
ЪЧ![]() ЕФКУЕу
ЕФКУЕу
![]()
![]()
![]()
Ђм![]() ЪЧ
ЪЧ![]() ЕФКУЕу
ЕФКУЕу
![]()
![]()
![]()
Д№ЃКЕБ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ40ЪБЃЌ
ЁЂ40ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жаЧЁгавЛИіЕуЮЊЦфгрСНЕуЕФКУЕуЃЎ
жаЧЁгавЛИіЕуЮЊЦфгрСНЕуЕФКУЕуЃЎ

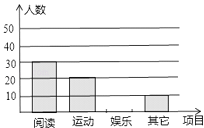
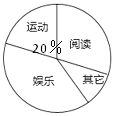
ЁОЬтФПЁПеХРЯЪІдЊЕЉНкЦкМфЕНЮфЩЬжкдВЩЬГЁЙКТђвЛЬЈФГЦЗХЦБЪМЧБОЕчФдЃЌЧЁЗъЩЬГЁе§ЭЦГіЁАгдЊЕЉЁБДйЯњДђелЛюЖЏЃЌОпЬхгХЛнЧщПіШчБэЃК
ЙКЮязмН№ЖюЃЈдМлЃЉ | елПл |
ВЛГЌЙ§5000дЊЕФВПЗж | ОХел |
ГЌЙ§5000дЊЧвВЛГЌЙ§10000дЊЕФВПЗж | АЫел |
ГЌЙ§10000дЊЧвВЛГЌЙ§20000дЊЕФВПЗж | Цпел |
ЁЁ | ЁЁ |
Р§ШчЃКШєЙКТђЕФЩЬЦЗдМлЮЊ15000дЊЃЌЪЕМЪИЖПюН№ЖюЮЊЃК
5000ЁС90%+ЃЈ10000Љ5000ЃЉЁС80%+ЃЈ15000Љ10000ЃЉЁС70%ЃН12000дЊЃЎ
ЃЈ1ЃЉШєетжжЦЗХЦЕчФдЕФдМлЮЊ8000дЊ/ЬЈЃЌЧыЧѓГіеХРЯЪІЪЕМЪИЖПюН№ЖюЃЛ
ЃЈ2ЃЉвбжЊеХРЯЪІЙКТђвЛЬЈИУЦЗХЦЕчФдЪЕМЪИЖЗб5700дЊЃЎ
ЂйЧѓИУЦЗХЦЕчФдЕФдМлЪЧЖрЩйдЊ/ЬЈЃП
ЂкШєЪлГіетЬЈЕчФдЩЬГЁШдПЩЛёРћ14%ЃЌЧѓетжжЦЗХЦЕчФдЕФНјМлЮЊЖрЩйдЊ/ЬЈЃП