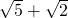Question

方程2x⁵+x⁴-20x³-10x²+2x+1=0有一个实数根是（　　）

• A、

  5

  +

  3

• B、

  5

  +

  2

• C、

  3

  +

  2

• D、

  5

  -

  3

Answer 1

分析：本题可用分解因式，提取公因式，实现了降次，再解方程求解．注意(

3

+

2

)2=5+2

6

，(-

3

-

2

)2=5+2

6

，(

3

-

2

)2=5-2

6

，(-

3

+

2

)2=5-2

6

．

解答：解：原方程可化为
（2x⁵-20x³+2x）+（x⁴-10x²+1）=0．
即（2x+1）（x⁴-10x²+1）=0．
∴2x+1=0或x⁴-10x²+1=0，
（1）当2x+1=0时，解得x=-

1

2

；
（2）当x⁴-10x²+1=0时，x²=

10+ 102-4

2

=5+ 2

6

，或x²=

10- 102-4

2

=5- 2

6

，
①当x²=5+ 2

6

，解得x=

3

+

2

或x=-

3

-

2

，
②当x²=5-2

6

，解得x=

3

-

2

或x=-

3+

2

，
综上所述x可能为-

1

2

、

3

+

2

、-

3

-

2

、

3

-

2

、-

3+

2

．
故选C．

点评：本题考查了高次方程的求解，解决本题主要是通过分解因式实现了降次，再对每个因式求解．