题目内容
如图，弦BC经过圆心D，AD⊥BC，AC交⊙D于E，AD交⊙D于M，BE交AD于N．求证：△BND∽△ABD．分析：首先证明△ABD≌△ACD，由全等三角形的性质可知：∠ABD=∠ACD因为BC是直径，所以∠BEC=90°再证明∠BND=∠ACD即可证明△ABD∽△ACD．
解答：证明：∵AD⊥BC，
∴∠ADB=∠ADC=90°，
∵在△ADB和△ADC中，
∴△ABD≌△ACD（SAS），
∴∠ABD=∠ACD，
∵BC是直径，
∴∠BEC=90°，
∵∠BND=∠ANE=90°-∠DAC=∠ACD，
∴△ABD∽△ACD．
∴∠ADB=∠ADC=90°，
∵在△ADB和△ADC中，
|
∴△ABD≌△ACD（SAS），
∴∠ABD=∠ACD，
∵BC是直径，
∴∠BEC=90°，
∵∠BND=∠ANE=90°-∠DAC=∠ACD，
∴△ABD∽△ACD．
点评：本题考查了全等三角形的判定和性质、圆周角定理以及讨论和相似三角形的判定，题目难度不大．
练习册系列答案
相关题目
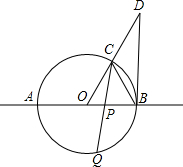如图，直线AB经过⊙O的圆心O，且与⊙O交于A、B两点，AB=4，半径OC的延长线与过点B的直线交于点D，OC=CD，BC=
如图，直线AB经过⊙O的圆心O，且与⊙O交于A、B两点，AB=4，半径OC的延长线与过点B的直线交于点D，OC=CD，BC=
OD．点Q为⊙O上一动点．
如图，弦BC经过圆心D，AD⊥BC，AC交⊙D于E，AD交⊙D于M，BE交AD于N．求证：△BND∽△ABD．