��Ŀ����
��ͼ����һ��ֱ�����ǰ��ֱ�Ƕ�������ƽ��ֱ������ϵ��ԭ��O����ֱ�DZ���������y=ax2��a��0������A��B���㣬�����������⣺

��1�������OA=OB=2 ����ͼ1������a��ֵ��
����ͼ1������a��ֵ��
��2����ͬһ�������ߣ������ǰ��Ƶ�O��ת����ͼ2��ʾλ��ʱ����B��BF��x���ڵ�F�����OF=1��д����ʱ��B�����꣬�����A�ĺ����ꣻ
��3���Ը������ߣ������ǰ��Ƶ�O��ת����Ƕ�ʱ������A��B�����߶��ܾ���һ���̶��ĵ㣬������õ�����꣮
�⣺��1�����߶�AB��y��Ľ���ΪC���������ߵĶԳ��Կɵ�CΪAB�е㣬
��OA=OB=2 ����AOB=90�㣬
����AOB=90�㣬
��AC=OC=BC=2����B��2��-2����
��B��2��-2������������y=ax2��a��0���ã�a=- ��
��
��2������A��AE��x���ڵ�E��
�ߵ�B�ĺ�����Ϊ1����B ��1��- ����
����
��A��-m��- m 2����m��0������
m 2����m��0������
OB2=12+�� ��2=
��2= ��OA2=m2+
��OA2=m2+ m4��AB2=��1+m��2+��-
m4��AB2=��1+m��2+��- +
+ m2��2��
m2��2��
�ߡ�AOB=90�㣬��AB2=OA2+OB2��
�ࣨ1+m��2+��- +
+ m2��2=m2+
m2��2=m2+ m4+
m4+ ��
��
��ã�m=0������������ȥ����m=4������A�ĺ�����Ϊ-4��
��3���ⷨһ����A��-m��- m 2����m��0����B��n��-
m 2����m��0����B��n��- n 2����n��0����
n 2����n��0����
��ֱ��AB�Ľ���ʽΪ��y=kx+b���� ��
��
�١�n+�ڡ�m�ã���m+n��b=- ��m2n+mn2��=-
��m2n+mn2��=- mn��m+n����
mn��m+n����
��b=- mn��
mn��
��ǰ��֪��OB2=n2+ n4��OA2=m2+
n4��OA2=m2+ m4��AB2=��n+m��2+��-
m4��AB2=��n+m��2+��- m2+
m2+ n2��2��
n2��2��
��AB2=OA2+OB2���ã�n2+ n4+m2+
n4+m2+ m4=��n+m��2+��-
m4=��n+m��2+��- m2+
m2+ n2��2��
n2��2��
����mn=4��
��b=- ��4=-2���ɴ˿�֪����kΪ��ֵ��ֱ��AB����㣨0��-2����
��4=-2���ɴ˿�֪����kΪ��ֵ��ֱ��AB����㣨0��-2����
�ⷨ������A��-m��- m 2����m��0����B��n��-
m 2����m��0����B��n��- n 2����n��0����
n 2����n��0����
ֱ��AB��y��Ľ���ΪC������S��AOB=S����ABFE-S��AOE-S��BOF=S��AOC+S��BOC���ɵ�
 ����
���� m2+
m2+ n2����m+n��-
n2����m+n��- m��
m�� m2-
m2- n��
n�� n2=
n2= CO•m+
CO•m+ CO•n
CO•n
����CO= mn��
mn��
��ǰ��֪��OB2=n2+ n4��OA2=m2+
n4��OA2=m2+ m4��AB2=��n+m��2+��-
m4��AB2=��n+m��2+��- m2+
m2+ n2��2��
n2��2��
��AB2=OA2+OB2���ã�n2+ n4+m2+
n4+m2+ m4=��n+m��2+��-
m4=��n+m��2+��- m2+
m2+ n2��2��
n2��2��
����mn=4��
��OC=2Ϊ�̶�ֵ����ֱ��AB�������y��Ľ���C��0��-2����
��������1�����������ߵĶԳ��ԣ������B�����꣬����������y=ax2��a��0����a��ֵ��
��2������A��AE��x���ڵ�E��������AB2=OA2+OB2�������A�ĺ����꣮
��3��������A��-m��- m2����m��0����B��n��-
m2����m��0����B��n��- n2����n��0������ʾ��ֱ��AB����ʽ��b=-
n2����n��0������ʾ��ֱ��AB����ʽ��b=- mn�������ù��ɶ����ó�mn=4�������ó�ֱ��AB�������y��Ľ���C��0��-2����
mn�������ù��ɶ����ó�mn=4�������ó�ֱ��AB�������y��Ľ���C��0��-2����
���������⿼���������ߵĶԳ��Ժ��ɶ����Լ�һԪ���η��̽ⷨ���ڣ�3�������mn=4�ǽ���Ĺؼ����ۺ��Խ�ǿ����һ�����Ѷȣ�
��OA=OB=2
 ����AOB=90�㣬
����AOB=90�㣬��AC=OC=BC=2����B��2��-2����
��B��2��-2������������y=ax2��a��0���ã�a=-
 ��
����2������A��AE��x���ڵ�E��
�ߵ�B�ĺ�����Ϊ1����B ��1��-
 ����
������A��-m��-
 m 2����m��0������
m 2����m��0������OB2=12+��
 ��2=
��2= ��OA2=m2+
��OA2=m2+ m4��AB2=��1+m��2+��-
m4��AB2=��1+m��2+��- +
+ m2��2��
m2��2���ߡ�AOB=90�㣬��AB2=OA2+OB2��
�ࣨ1+m��2+��-
 +
+ m2��2=m2+
m2��2=m2+ m4+
m4+ ��
����ã�m=0������������ȥ����m=4������A�ĺ�����Ϊ-4��
��3���ⷨһ����A��-m��-
 m 2����m��0����B��n��-
m 2����m��0����B��n��- n 2����n��0����
n 2����n��0������ֱ��AB�Ľ���ʽΪ��y=kx+b����
 ��
���١�n+�ڡ�m�ã���m+n��b=-
 ��m2n+mn2��=-
��m2n+mn2��=- mn��m+n����
mn��m+n������b=-
 mn��
mn����ǰ��֪��OB2=n2+
 n4��OA2=m2+
n4��OA2=m2+ m4��AB2=��n+m��2+��-
m4��AB2=��n+m��2+��- m2+
m2+ n2��2��
n2��2����AB2=OA2+OB2���ã�n2+
 n4+m2+
n4+m2+ m4=��n+m��2+��-
m4=��n+m��2+��- m2+
m2+ n2��2��
n2��2������mn=4��

��b=-
 ��4=-2���ɴ˿�֪����kΪ��ֵ��ֱ��AB����㣨0��-2����
��4=-2���ɴ˿�֪����kΪ��ֵ��ֱ��AB����㣨0��-2�����ⷨ������A��-m��-
 m 2����m��0����B��n��-
m 2����m��0����B��n��- n 2����n��0����
n 2����n��0����ֱ��AB��y��Ľ���ΪC������S��AOB=S����ABFE-S��AOE-S��BOF=S��AOC+S��BOC���ɵ�
 ����
���� m2+
m2+ n2����m+n��-
n2����m+n��- m��
m�� m2-
m2- n��
n�� n2=
n2= CO•m+
CO•m+ CO•n
CO•n����CO=
 mn��
mn����ǰ��֪��OB2=n2+
 n4��OA2=m2+
n4��OA2=m2+ m4��AB2=��n+m��2+��-
m4��AB2=��n+m��2+��- m2+
m2+ n2��2��
n2��2����AB2=OA2+OB2���ã�n2+
 n4+m2+
n4+m2+ m4=��n+m��2+��-
m4=��n+m��2+��- m2+
m2+ n2��2��
n2��2������mn=4��
��OC=2Ϊ�̶�ֵ����ֱ��AB�������y��Ľ���C��0��-2����
��������1�����������ߵĶԳ��ԣ������B�����꣬����������y=ax2��a��0����a��ֵ��
��2������A��AE��x���ڵ�E��������AB2=OA2+OB2�������A�ĺ����꣮
��3��������A��-m��-
 m2����m��0����B��n��-
m2����m��0����B��n��- n2����n��0������ʾ��ֱ��AB����ʽ��b=-
n2����n��0������ʾ��ֱ��AB����ʽ��b=- mn�������ù��ɶ����ó�mn=4�������ó�ֱ��AB�������y��Ľ���C��0��-2����
mn�������ù��ɶ����ó�mn=4�������ó�ֱ��AB�������y��Ľ���C��0��-2�������������⿼���������ߵĶԳ��Ժ��ɶ����Լ�һԪ���η��̽ⷨ���ڣ�3�������mn=4�ǽ���Ĺؼ����ۺ��Խ�ǿ����һ�����Ѷȣ�

��ϰ��ϵ�д�
�����Ŀ
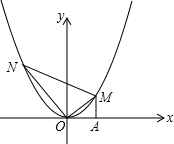 ����M��N�ĺ�����ֱ�Ϊm��n��m��0��n��0���������������⣺
����M��N�ĺ�����ֱ�Ϊm��n��m��0��n��0���������������⣺
 ����M��N���㣬��M��N�ĺ�����ֱ�Ϊm��n��m��0��n��0���������������⣺
����M��N���㣬��M��N�ĺ�����ֱ�Ϊm��n��m��0��n��0���������������⣺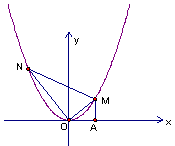

 ����ͼ1������a��ֵ��
����ͼ1������a��ֵ��