题目内容
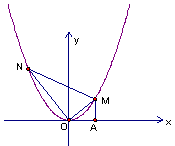
如图,将一把直角三角板的直角顶点放置于原点O,两直角边与抛物线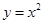 交于M、N两点,设M、N的横坐标分别为m、n(m﹥0,n﹤0);请解答下列问题:
交于M、N两点,设M、N的横坐标分别为m、n(m﹥0,n﹤0);请解答下列问题:【小题1】当m=1时,n=__ ▲ ; 当m=2时,n=__ ▲ 试猜想m与n满足的关系,并证明你猜想的结论。
【小题2】连接M、N,若△OMN的面积为S,求S关于m的函数关系式。
【小题3】当三角板绕点O旋转到某一位置时,恰好使得∠MNO=30°,此时过M作MA⊥x轴,垂足为A,求出△OMA的面积
【小题4】当m=2时,抛物线上是否存在一点P使M、N、O、P四点构成梯形,若存在,直接写出所有满足条件的点P的坐标;若不存在,说明理由。
【小题1】当m=1时,n= -1;(1分)当m=2时,n=
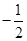 ;(1分)
;(1分) m与n满足的关系:
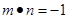 (1分)
(1分)证明:作NB⊥x轴,垂足为B,则△OMA∽△NOB;∵M(
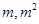 ) N
) N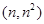 ∴
∴ 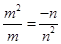
整理得:
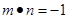 (1分)
(1分)【小题2】S=
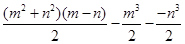 =
=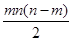 =
=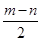 =
=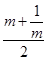 =
= (2分)
(2分)(注:还有其他方法)
【小题3】∵∠MNO=30°,∴
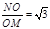 又∵△OMA∽△NOB,∴
又∵△OMA∽△NOB,∴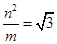 (1分)
(1分)将
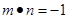 代入得
代入得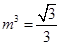 (1分)
(1分)∴△OMA的面积=
 =
=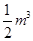 =
=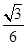 (1分)
(1分)【小题4】
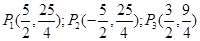 (3分)解析:
(3分)解析:(1)作NB⊥x轴,垂足为B,利用△OMA∽△NOB,推出
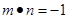 ;
;(2)根据三角形的面积公式及(1)的结论得出S关于m的函数关系式;
(3)利用△OMA∽△NOB算出
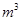 的值,然后根据三角形面积公式得出结果;
的值,然后根据三角形面积公式得出结果;(4)P点有三种可能,PO∥MN,PN∥OM,PM∥NO,利用平行线计算出P点的坐标.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
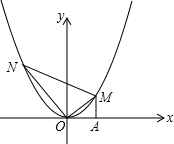 ,设M、N的横坐标分别为m、n(m>0,n<0);请解答下列问题:
,设M、N的横坐标分别为m、n(m>0,n<0);请解答下列问题:

 (如图1),求a的值;
(如图1),求a的值;
 (如图1),求a的值;
(如图1),求a的值;