题目内容
(1)若sin(α+45°)=
,则cos(45°-α)的值为
;
(2)若tanα=3,则
=
.
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(2)若tanα=3,则
| sinα-cosα |
| 2sinα+cosα |
| 2 |
| 7 |
| 2 |
| 7 |
分析:(1)根据sin(α+45°)=
,求得α的值,将α代入cos(45°-α)求值即可;
(2)做出直角三角形ABC,根据tanα=3,设AB=1,BC=3,根据勾股定理求得AC的值,然后求出sinα和cosα代入计算即可.
| ||
| 2 |
(2)做出直角三角形ABC,根据tanα=3,设AB=1,BC=3,根据勾股定理求得AC的值,然后求出sinα和cosα代入计算即可.
解答:解:(1)∵sin(α+45°)=
,
∴α+45°=60°,
则α=15°,
∴cos(45°-α)=cos30°=
;
(2)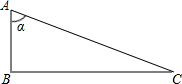
根据tanα=3,设AB=1,BC=3,
则AC=
=
,
则sinα=
=
=
,
cosα=
=
,
则
=
=
.
故答案为:
,
.
| ||
| 2 |
∴α+45°=60°,
则α=15°,
∴cos(45°-α)=cos30°=
| ||
| 2 |
(2)

根据tanα=3,设AB=1,BC=3,
则AC=
| 12+32 |
| 10 |
则sinα=
| BC |
| AC |
| 3 | ||
|
3
| ||
| 10 |
cosα=
| AB |
| AC |
| 1 | ||
|
则
| sinα-cosα |
| 2sinα+cosα |
| ||||||||
2×
|
| 2 |
| 7 |
故答案为:
| ||
| 2 |
| 2 |
| 7 |
点评:本题考查了特殊角的三角函数值以及同角三角函数的关系,难度适中,解答本题的关键是熟练掌握几个特殊角的三角函数值以及同角三角函数的关系.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目

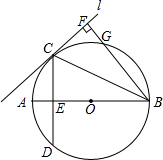 为F,BF交⊙O于C.
为F,BF交⊙O于C.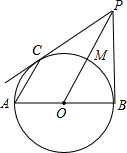 如图,AB是⊙O的直径,点C在⊙O上,M是
如图,AB是⊙O的直径,点C在⊙O上,M是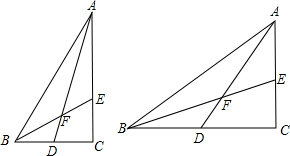 ,交AD于F.
,交AD于F.