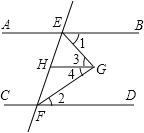
题目内容
【题目】在
中，
，
，点
是
中点，点
在
上，
，将
沿着
翻折，点
的对应点是点
，直线
与交于点
，那么
的面积
__________．
【答案】
或
【解析】
通过计算E到AC的距离即EH的长度为3，所以根据DE的长度有两种情况：①当点D在H点上方时，②当点D在H点下方时，两种情况都是过点E作
交AC于点E，过点G作
交AB于点Q，利用含30°的直角三角形的性质和勾股定理求出AH,DH的长度，进而可求AD的长度，然后利用角度之间的关系证明
，再利用等腰三角形的性质求出GQ的长度，最后利用
即可求解．
①当点D在H点上方时，
过点E作交AC于点E，过点G作交AB于点Q，
，点
是
中点，
．
∵，
．
，
，
．
，
，
，
，
，
．
由折叠的性质可知，
，
，
，
．
又
，
．
，
．
，
即
，
．
，
；
②当点D在H点下方时，
过点E作交AC于点E，过点G作交AB于点Q，
，点是中点，
．
∵，
．
，
，
．
，
，
，
，
，
．
由折叠的性质可知，
，
，
，
．
又 ，
．
，
．
，
即，
．
，
，
综上所述，
的面积为或．
故答案为：或．
练习册系列答案
阅读快车系列答案
相关题目
