题目内容
如图，DE∥AC，∠D=60°．下列结论正确的是
- A.∠ABD=30°
- B.∠ABD=60°
- C.∠CBD=100°
- D.∠CBD=140°
B
分析：根据平行线的性质由DE∥AC得∠ABD=∠D=60°，然后根据平角的定义得到计算∠CBD．
解答：∵DE∥AC，
∴∠ABD=∠D=60°，
∴∠CBD=180°-∠ABD=120°．
故选B．
点评：本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．
分析：根据平行线的性质由DE∥AC得∠ABD=∠D=60°，然后根据平角的定义得到计算∠CBD．
解答：∵DE∥AC，
∴∠ABD=∠D=60°，
∴∠CBD=180°-∠ABD=120°．
故选B．
点评：本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
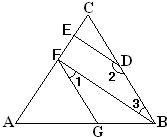24、已知如图，DE⊥AC，∠AGF=∠ABC，∠1+∠2=180°，试判断BF与AC的位置关系，并说明理由．
已知：如图，DE⊥AC，BF⊥AC，且DC=AB，DC∥AB，AE=CF
如图，DE⊥AC于点E，BF⊥AC于点F，∠1+∠2=180°，试判断∠AGF与∠ABC的大小关系，并说明理由．
已知，如图，DE∥AC，DF∥BC，∠A=55°，∠B=65°，求∠FDE的度数．