Question

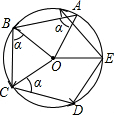
如图所示，小华从一个圆形场地的A点出发，沿着与半径OA夹角为α的方向行走，走到场地边缘B后，再沿着与半径OB夹角为α的方向折向行走．按照这种方式，小华第五次走到场地边缘时处于弧AB上，此时∠AOE=56°，则α的度数是（　　）

• A、52°
• B、60°
• C、72°
• D、76°

Answer 1

分析：根据圆心角是360度，即可求得∠AOB=76°，再根据等腰三角形的性质可求∠α=∠BAO=

180°-76°

2

=52°．

解答：解：连接OC，OD，
∵∠BAO=∠CBO=∠DCO=∠EDO=α，
∵OA=OB=OC，
∴∠ABO=∠BCO=α，
∴∠AOB=∠BOC=∠COD=∠DOE=180°-2α，
∴4∠AOB+∠AOE=360°，
∴∠AOB=76°，
∴在等腰三角形AOB中，
∠α=∠BAO=

180°-76°

2

=52°．
故选A．

点评：本题利用了等腰三角形的性质和三角形的内角和定理及一个周角为360°求解．