Question

【题目】如图，Rt△APE，∠AEP＝90°，以AB为直径的⊙，O交PE于C，且AC平分∠EAP．连接BC，PB：PC＝1：2．

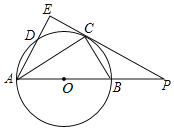
（1）求证：PE是⊙O的切线；

（2）已知⊙O的半径为，求AE的长．

Answer 1

【答案】（1）见解析；（2）4

【解析】

（1）连接OC，由AC平分∠EAP，得到∠DAC=∠OAC，由等腰三角形的性质得到∠CAO=∠ACO，等量代换得到∠DAC=∠ACO，根据平行线的性质得到∠E=∠OCP=90°，于是得到结论；

（2）设PB=x，PC=2x，根据勾股定理得到PC=，求得AP=，根据相似三角形的性质即可得到结论．

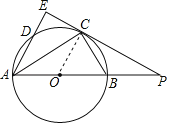
解：（1）连接OC，

∵AC平分∠EAP，

∴∠DAC＝∠OAC，

∵OA＝OC，

∴∠CAO＝∠ACO，

∴∠DAC＝∠ACO，

∴AE∥OC，

∴∠E＝∠OCP＝90°

∴PE是⊙O的切线；.

（2）∵PB：PC＝1：2，

∴设PB＝x，PC＝2x，

∵OC2+PC2＝OP2，即（）2+（2x）2＝（+x）2，

∴x＝，.

∴PC＝，PB＝，

∴AP＝，.

∵OC∥AE，

∴△PCO∽△PEA，

∴

∴AE＝4．