题目内容
2. 如图,点A,B分别在函数y=$\frac{{k}_{1}}{x}$(k1>0)与y=$\frac{{k}_{2}}{x}$(k2<0)的图象上,线段AB的中点M在y轴上.若△AOB的面积为2,则k1-k2的值是4.
如图,点A,B分别在函数y=$\frac{{k}_{1}}{x}$(k1>0)与y=$\frac{{k}_{2}}{x}$(k2<0)的图象上,线段AB的中点M在y轴上.若△AOB的面积为2,则k1-k2的值是4.
分析 设A(a,b),B(-a,d),代入双曲线得到k1=ab,k2=-ad,根据三角形的面积公式求出ad+ad=4,即可得出答案.
解答 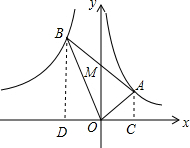 解:作AC⊥x轴于C,BD⊥x轴于D,
解:作AC⊥x轴于C,BD⊥x轴于D,
∴AC∥BD∥y轴,
∵M是AB的中点,
∴OC=OD,
设A(a,b),B(-a,d),
代入得:k1=ab,k2=-ad,
∵S△AOB=2,
∴$\frac{1}{2}$(b+d)•2a-$\frac{1}{2}$ab-$\frac{1}{2}$ad=2,
∴ab+ad=4,
∴k1-k2=4,
故选:4.
点评 本题主要考查对反比例函数系数的几何意义,反比例函数图象上点的坐标特征,三角形的面积等知识点的理解和掌握,能求出ab+ad=4,4是解此题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
12. 如图所示,射线OP表示的方向是( )
如图所示,射线OP表示的方向是( )
 如图所示,射线OP表示的方向是( )
如图所示,射线OP表示的方向是( )| A. | 南偏西25° | B. | 南偏东25° | C. | 南偏西65° | D. | 南偏东65° |
11.下列方程中,解为x=2的是( )
| A. | 3x+6=3 | B. | -x+6=2x | C. | 4-2(x-1)=1 | D. | $\frac{1}{2}x+2=0$ |
 如图,已知正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.给出以下结论:
如图,已知正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.给出以下结论: