题目内容
如图所示，（1）若DE∥BC，则可得到：
①∠1=
∠B
∠B
，根据两直线平行，同位角相等
两直线平行，同位角相等
；②∠2=
∠5
∠5
，根据两直线平行，内错角相等
两直线平行，内错角相等
；③∠4+
∠B
∠B
=180°，根据两直线平行，同旁内角互补
两直线平行，同旁内角互补
．（2）若EF∥AB，则可得到：
①∠1=
∠2
∠2
；②∠B=∠5
∠5
； ③∠2+∠4
∠4
=180°．分析：根据平行线的性质两直线平行，同位角相等； 两直线平行，内错角相等；两直线平行，同旁内角互补进行解答即可．
解答：解：（1）∵DE∥BC，∴∠1=∠B（两直线平行，同位角相等）；
∠2=∠5（两直线平行，内错角相等）；
∠4+∠B=180°（两直线平行，同旁内角互补）；
（2）∵FE∥AB，∴∠1=∠2（两直线平行，内错角相等），
∠B=∠5（两直线平行，同位角相等）；
∠2+∠4=180°（两直线平行，同旁内角互补）．
∠2=∠5（两直线平行，内错角相等）；
∠4+∠B=180°（两直线平行，同旁内角互补）；
（2）∵FE∥AB，∴∠1=∠2（两直线平行，内错角相等），
∠B=∠5（两直线平行，同位角相等）；
∠2+∠4=180°（两直线平行，同旁内角互补）．
点评：此题主要考查了平行线的性质，关键是熟练掌握性质定理．
练习册系列答案
相关题目
18、按如图所示的程序计算，若开始输入的x的值为48，我们发现第一次得到的结果为24，第2次得到的结果为12，…，请你探索第2009次得到的结果为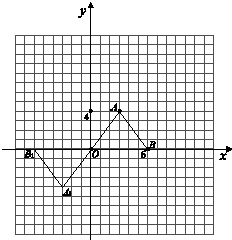
22、在平面直角坐标系中，△AOB的位置如图所示．
9、用5个一样大小的小长方形恰好可以拼成如图所示的大长方形，若大长方形的周长是14，则小长方形的长是