题目内容
【题目】如图,点A,B是数轴上的两个点,点A表示的数为﹣2,点B在点A右侧,距离A点12个单位长度,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.

(1)填空:①数轴上点B表示的数为 ;
②数轴上点P表示的数为 (用含t的代数式表示).
(2)设AP和PB的中点分别为点M,N,在点P的运动过程中,线段M N的长度是否发生变化?若变化,请说明理由;若不变,求出线段M N的长.
【答案】(1)①数轴上点B表示的数为10;②数轴上点P表示的数为 (2t﹣2);(2)线段MN的长度不发生变化,值为6.
【解析】
(1)①利用两点之间的距离计算方法求得点B所表示的数即可;
②利用左减右加的规律求得点P的所表示的数即可;
(2)分类讨论:①当点P在点A、B两点之间运动时,②当点P运动到点B的右侧时,③点P运动到点B时,利用中点的定义和线段的和差易求出MN.
解:(1)①∵10-(-2)=12,
∴数轴上点B表示的数为10;
②数轴上点P表示的数为(2t﹣2);
(2)线段MN的长度不发生变化.
①如图,当点P在点A、B之间运动时,
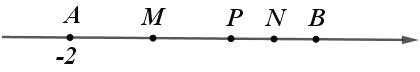
MN = MP + NP =![]() AP + PB =
AP + PB =![]() AB =
AB =![]() ×12 = 6;
×12 = 6;
②当点P运动到点B的右侧时,
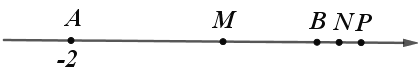
MN = MP﹣PB = ![]() AP﹣
AP﹣![]() BP =
BP = ![]() (AP﹣PB)
(AP﹣PB)
= ![]() AB =
AB = ![]() ×12 = 6;
×12 = 6;
③当点P运动到点B时,MN = MB = ![]() AB =
AB = ![]() ×12 = 6;
×12 = 6;
综上所述,线段MN的长度不发生变化,值为6.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目