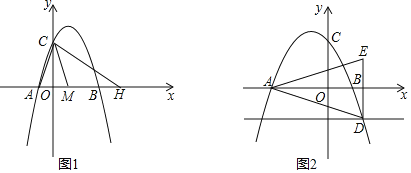Question

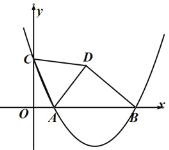
【题目】如图，在平面直角坐标系中，点C是y轴正半轴上的一个动点，抛物线y＝ax2－6ax+5a（a是常数，且a＞0）过点C，与x轴交于点A、B，点A在点B的左边．连接AC，以AC为边作等边三角形ACD，点D与点O在直线AC两侧，连接BD，则BD的最小值是_________．

Answer 1

【答案】3

【解析】

由抛物线的性质先求三点坐标，过点D作DE⊥AC于点E，过点D作x轴的垂线于点H，过点E作EF∥x轴交y轴于点F交DH于点G，利用等边三角形与相似三角形的性质求解的坐标，利用两点间距离公式建立与之间的函数关系式，利用函数性质求的最小值．

解：

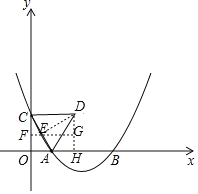
如图，过点D作DE⊥AC于点E，过点D作x轴的垂线于点H，过点E作EF∥x轴交y轴于点F交DH于点G，

∵△ACD为等边三角形，则点E为AC的中点，

则点E（ ），AE=CE=ED，

∵∠CEF+∠FCE=90°，∠CEF+∠DEG=90°，

∴∠DEG=∠ECF，

∴△CFE∽△EGD，

∴

为中点，轴，

解得：GE=，DG=

故点D（ ），

故当时，的最小值

的最小值为 （负根舍去）

故答案为：