题目内容
一艘船向正东先航行,上午十点在灯塔的西南方向五十海里处,到下午两点时,航行到灯塔的东偏南60°的方向,画出船的航行方位图并求出船的航行速度.
考点:解直角三角形的应用-方向角问题
专题:
分析:按照题意作出图形,根据题意即可求得BD和CD的长,根据时间和BC的长即可解题.
解答:解:按照题意作出图形,

由题意得:∠BAD=45°,AB=50海里,∠CAD=60°,
∴AD=50•cos45°=25
海里,
∴BD=25
海里,
∵tan∠DAC=
=
,
∴CD=25
海里,
∴BC=25
+25
海里,
∴船的速度为
海里/小时.
答:船的速度为
海里/小时.

由题意得:∠BAD=45°,AB=50海里,∠CAD=60°,
∴AD=50•cos45°=25
| 2 |
∴BD=25
| 2 |
∵tan∠DAC=
| CD |
| AD |
| 3 |
∴CD=25
| 6 |
∴BC=25
| 2 |
| 6 |
∴船的速度为
25
| ||||
| 4 |
答:船的速度为
25
| ||||
| 4 |
点评:本题考查了直角三角形中三角函数的运用,考查了特殊角的三角函数值,本题中求得BD,CD的长是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果一个有理数的绝对值是5,那么这个数一定是( )
| A、5 | B、-5 |
| C、-5或5 | D、以上都不对 |
 如图,AB=AC,AD=AE,则图中全等的三角形的对数共有( )对.
如图,AB=AC,AD=AE,则图中全等的三角形的对数共有( )对.| A、2对 | B、3对 | C、4对 | D、5对 |
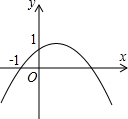 如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0),下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>-1时,y>0.其中正确结论的个数是:
如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0),下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>-1时,y>0.其中正确结论的个数是: 棱长为a的正方体摆放成如图的形状:
棱长为a的正方体摆放成如图的形状: 如图,MN是过点A的直线,则图中有一个端点是点A的线段有
如图,MN是过点A的直线,则图中有一个端点是点A的线段有