题目内容
20. 如图,△ABC是等边三角形,D、E分别为BC、AC上一点,且BD=CE,AD交BE于F.
如图,△ABC是等边三角形,D、E分别为BC、AC上一点,且BD=CE,AD交BE于F.(1)求证:AD=BE;
(2)若∠CFE=30°,求$\frac{BD}{CD}$的值.
分析 (1)根据等边三角形性质得出AB=BC,∠ABD=∠C=60°,再根据SAS可得△ABD≌△BCE,根据全等三角形的性质得到结论;
(2)由△ABD≌△BCE,可证得∠BAD=∠CBE,进一步得到∠EAF=∠ABE,然后根据有两角对应相等的三角形相似,即可得△AEF∽△ABE.
解答 解:(1)∵△ABC为等边三角形,
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠C}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△BCE(SAS),
∴AD=BE;
(2)如图,连接DE,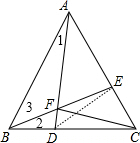
由(1)得:∠1=∠2,
∴∠AFE=∠1+∠3=∠2+∠3=60°,
∵∠ACD=60°,
∴∠AFE=∠ACD,
∵∠FAE=∠CAD,
∴∵△AFE∽△ACD,
∴$\frac{AF}{AC}=\frac{AE}{AD}$,
∴$\frac{AF}{AE}=\frac{AC}{AD}$,
∵∠FAC=∠EAD,
∴△FAC∽△EAD,
∴∠AFC=∠AED,
∵∠AFC=∠AFE+∠CFE=60°+30°=90°,
∴∠AED=90°,
∴CED=90°,
∵∠DCE=60°,
∴∠CDE=30°,
∴CE=$\frac{1}{2}$CD,
∵BD=CE,
∴BD=$\frac{1}{2}$CD,
∴$\frac{BD}{CD}=\frac{1}{2}$.
点评 本题考查了全等三角形的判定和性质,关键是根据等边三角形的性质:等边三角形的三个内角都相等,且都等于60°;三条边相等分析.

练习册系列答案
相关题目
 如图,正方形ABCD的边长为6cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于2或4cm.
如图,正方形ABCD的边长为6cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于2或4cm. 已知一次函数y1=2x-3与y2=-x+4的图象相交于点P,它们与y轴交于A、B两点.
已知一次函数y1=2x-3与y2=-x+4的图象相交于点P,它们与y轴交于A、B两点.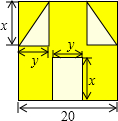 “囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
“囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
 +(-3x2+5x-7)=-2x2+3x-6
+(-3x2+5x-7)=-2x2+3x-6 如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.
如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.