题目内容
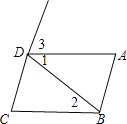
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线BE、CF相交于点P.
(1)若∠ABC=70°,∠ACB=50°,则∠BPC= °;
(2)求证:∠BPC=180°﹣![]() (∠ABC+∠ACB);
(∠ABC+∠ACB);
(3)若∠A=α,求∠BPC的度数.

【答案】(1)120°;(2)证明见解析;(3)∠BPC=90°+![]()
![]() .
.
【解析】试题分析:(1)根据已知条件求出∠ABC+∠ACB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形的内角和等于180°列式计算即可得解;(2)根据三角形的内角和和角平分线的定义即可得到结论;(3)根据三角形的内角和和角平分线的定义即可得到结论.
试题解析:(1)PBC+∠PCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() ×120°=60°,
×120°=60°,
在△PBC中,∠BPC=180°(∠PBC+∠PCB)=180°60°=120°
故答案为:120;
(2)证明:∵∠ABC和∠ACB的平分线BE、CF相交于点P,
∴∠PBC=![]() ∠ABC, ∠PCB=
∠ABC, ∠PCB=![]() ∠ACB,
∠ACB,
∵∠BPC +∠PBC+∠PCB=180°,
∴∠BPC=180°-(∠PBC+∠PCB)= 180°-(![]() ∠ABC +
∠ABC +![]() ∠ACB) =180°-
∠ACB) =180°-![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
∴∠BPC=180°-![]() (∠ABC+∠ACB);
(∠ABC+∠ACB);
(3)在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°-∠A,
∵由(2)可知:∠BPC=180°-![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
∴∠BPC=180°-![]() (180°-∠A),
(180°-∠A),
∵∠A= ![]() ,
,
∴∠BPC=180°-![]() (180°-
(180°- ![]() )=90°+
)=90°+![]()
![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目