题目内容
有一张矩形纸片ABCD,其中AD=8cm,上面有一个以AD为直径的半圆,正好与对边BC相切.如图(甲).将它沿DE折叠,使A点落在BC上,如图(乙),这时,半圆还露在外面的部分(阴影部分)的面积是( )
A.(π-
 )cm2
)cm2B.(
 π-
π- )cm2
)cm2C.(
 π+
π+ )cm2
)cm2D.(
 π+
π+ )cm2
)cm2
【答案】分析:如图,露在外面部分的面积可用扇形ODK与△ODK的面积差来求得.在Rt△ADC中,可根据AD即圆的直径和CD即圆的半径长,求出∠DAC的度数,进而得出∠ODA和∠ODK的度数,即可求得△ODK和扇形ODK的面积,由此可求得阴影部分的面积.
解答: 解:∵以AD为直径的半园,正好与对边BC相切,
解:∵以AD为直径的半园,正好与对边BC相切,
∴AD=2CD,
∵∠C=90°,
∴∠DAC=30°,
∴∠ADC=60°,
∴∠DOK=120°,
∴扇形ODK的面积为 πcm2,
πcm2,
作OH⊥DK于H,
∵∠D=∠K=30°,OD=4cm,
∴OH=2cm,DH=2 cm;
cm;
∴△ODK的面积为 4 cm2
cm2
∴半圆还露在外面的部分(阴影部分)的面积是( π-4
π-4 )cm2.
)cm2.
故选B.
点评:此题考查了折叠问题,解题时要注意找到对应的等量关系;还考查了圆的切线的性质,垂直于过切点的半径;还考查了直角三角形的性质,直角三角形中,如果有一条直角边是斜边的一半,那么这条直角边所对的角是30度.
解答:
 解:∵以AD为直径的半园,正好与对边BC相切,
解:∵以AD为直径的半园,正好与对边BC相切,∴AD=2CD,
∵∠C=90°,
∴∠DAC=30°,
∴∠ADC=60°,
∴∠DOK=120°,
∴扇形ODK的面积为
 πcm2,
πcm2,作OH⊥DK于H,
∵∠D=∠K=30°,OD=4cm,
∴OH=2cm,DH=2
 cm;
cm;∴△ODK的面积为 4
 cm2
cm2∴半圆还露在外面的部分(阴影部分)的面积是(
 π-4
π-4 )cm2.
)cm2.故选B.
点评:此题考查了折叠问题,解题时要注意找到对应的等量关系;还考查了圆的切线的性质,垂直于过切点的半径;还考查了直角三角形的性质,直角三角形中,如果有一条直角边是斜边的一半,那么这条直角边所对的角是30度.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
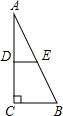 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( ) 如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一
如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一




 = ;
= ; 




 = ;
= ; 