题目内容
如图,矩形ABCD在平面直角坐标系xOy中,BC边在x轴上,点A(-1,2),点C(3,0).动点P从点A出发,以每秒1个单位的速度沿AD向点D运动,到达点D后停止.把BP的中点M绕点P逆时针旋转90°到点N,连接PN,DN.设P的运动时间为t秒.(1)经过1秒后,求出点N的坐标;
(2)当t为何值时,△PND的面积最大?并求出这个最大值;
(3)求在整个过程中,点N运动的路程是多少?

【答案】分析:(1)首先证明△BAP∽△PQN进而得出 ,利用A,C坐标得出PQ=1,NQ=
,利用A,C坐标得出PQ=1,NQ= ,即可得出答案;
,即可得出答案;
(2)首先表示出NQ= ,PD=4-t,再利用△PND的面积为y=
,PD=4-t,再利用△PND的面积为y= 进而利用二次函数最值求出即可;
进而利用二次函数最值求出即可;
(3)求出P点在A,D两点时N点位置,再利用勾股定理求出即可.
解答: 解:(1)当t=1时,AP=1,过点N作NQ⊥AD于点Q,
解:(1)当t=1时,AP=1,过点N作NQ⊥AD于点Q,
∵把BP的中点M绕点P逆时针旋转90°到点N,
∴∠BPN=90°,
∴∠APB+∠QPN=90°,
∵∠PQN=90°,
∴∠QPN+∠QNP=90°,
∴∠APB=∠QNP,
又∵∠A=∠PQN=90°,
∴△BAP∽△PQN,
∴ ,
,
∴PQ=1,NQ= ,
,
∴N(1, );
);
(2)当点P运动时间为t秒时,
∵点A(-1,2),点C(3,0),
∴NQ= ,PD=4-t,
,PD=4-t,
∴△PND的面积=y= =
= =-
=- (t-2)2+1,
(t-2)2+1,
当t=2时,y最大,
y最大=1.
(3)因为PQ=1,AP=t,点A(-1,2),
所以N(t,2- ),
),
当t=0时,2- =2;则N点坐标为(0,2),
=2;则N点坐标为(0,2),
当t=4时,2- =0,则N′点坐标为(4,0),并且点N沿直线y=2-
=0,则N′点坐标为(4,0),并且点N沿直线y=2- 运动,
运动,
所以:点N运动的路程是:NN′= =
= .
.
点评:此题主要考查了相似三角形的综合应用以及二次函数最值问题等知识,正确利用数形结合得出N点移动路线是解题关键.
 ,利用A,C坐标得出PQ=1,NQ=
,利用A,C坐标得出PQ=1,NQ= ,即可得出答案;
,即可得出答案;(2)首先表示出NQ=
 ,PD=4-t,再利用△PND的面积为y=
,PD=4-t,再利用△PND的面积为y= 进而利用二次函数最值求出即可;
进而利用二次函数最值求出即可;(3)求出P点在A,D两点时N点位置,再利用勾股定理求出即可.
解答:
 解:(1)当t=1时,AP=1,过点N作NQ⊥AD于点Q,
解:(1)当t=1时,AP=1,过点N作NQ⊥AD于点Q,∵把BP的中点M绕点P逆时针旋转90°到点N,
∴∠BPN=90°,
∴∠APB+∠QPN=90°,
∵∠PQN=90°,
∴∠QPN+∠QNP=90°,
∴∠APB=∠QNP,
又∵∠A=∠PQN=90°,
∴△BAP∽△PQN,
∴
 ,
,∴PQ=1,NQ=
 ,
,∴N(1,
 );
);(2)当点P运动时间为t秒时,
∵点A(-1,2),点C(3,0),
∴NQ=
 ,PD=4-t,
,PD=4-t,∴△PND的面积=y=
 =
= =-
=- (t-2)2+1,
(t-2)2+1,当t=2时,y最大,
y最大=1.

(3)因为PQ=1,AP=t,点A(-1,2),
所以N(t,2-
 ),
),当t=0时,2-
 =2;则N点坐标为(0,2),
=2;则N点坐标为(0,2),当t=4时,2-
 =0,则N′点坐标为(4,0),并且点N沿直线y=2-
=0,则N′点坐标为(4,0),并且点N沿直线y=2- 运动,
运动,所以:点N运动的路程是:NN′=
 =
= .
.点评:此题主要考查了相似三角形的综合应用以及二次函数最值问题等知识,正确利用数形结合得出N点移动路线是解题关键.

练习册系列答案
相关题目
 (2013•太原)如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线y=
(2013•太原)如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线y=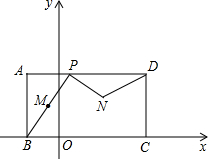 BP的中点M绕点P逆时针旋转90°到点N,连接PN,DN.设P的运动时间为t秒.
BP的中点M绕点P逆时针旋转90°到点N,连接PN,DN.设P的运动时间为t秒.
 如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线y=
如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线y= x-1经过点C交x轴于点E,双曲线y=
x-1经过点C交x轴于点E,双曲线y= 经过点D,则k的值为 .
经过点D,则k的值为 . 经过点C交x轴于点E,双曲线
经过点C交x轴于点E,双曲线 经过点D,则k的值为 .
经过点D,则k的值为 .