题目内容
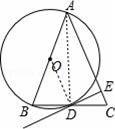
如图,在等腰△ABC中,AB=AC,以AB为直径作⊙O交底边BC于D.
(1)求证:BD=CD;
(2)若AB=3,cos∠ABC=
 ,在腰AC上取一点E使AE=
,在腰AC上取一点E使AE=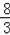
 ,试判断DE与⊙O的位置关系,并证明.
,试判断DE与⊙O的位置关系,并证明.
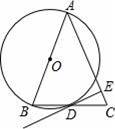

【考点】切线的判定;等腰三角形的性质;圆周角定理.
【专题】证明题.
【分析】(1)连结AD,如图,根据圆周角角定理,由AB为直径得∠ADB=90°,然后根据等腰三角形的性质可得BD=CD;
(2)连结OD,如图,在Rt△ABD中,先利用余弦定义计算出BD=
 AB=1,则Cd=1,再利用勾股定理计算出AD=2
AB=1,则Cd=1,再利用勾股定理计算出AD=2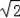
 ,则有
,则有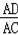

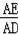
 =
=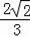
 ,加上∠DAE=∠CAD,于是可判断△ADE∽△ACD,所以∠AED=∠ADC=90°,接着证明OD为△ABC的中位线得到OD∥AC,所以OD⊥DE,则根据切线的判定定理可判断DE为⊙O的切线.
,加上∠DAE=∠CAD,于是可判断△ADE∽△ACD,所以∠AED=∠ADC=90°,接着证明OD为△ABC的中位线得到OD∥AC,所以OD⊥DE,则根据切线的判定定理可判断DE为⊙O的切线.
【解答】(1)证明:连结AD,如图,
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
而AB=AC,
∴BD=CD;
(2)解:DE与⊙O相切.理由如下:
连结OD,如图,
在Rt△ABD中,∵cos∠ABD=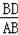
 =
=
 ,
,
∴BD=
 AB=
AB=
 ×3=1,
×3=1,
∴AD=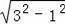
 =2
=2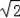
 ,CD=1,
,CD=1,
∵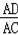
 =
=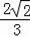
 ,
,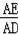
 =
=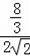
 =
=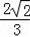
 ,
,
∴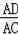
 =
=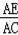
 ,
,
而∠DAE=∠CAD,
∴△ADE∽△ACD,
∴∠AED=∠ADC=90°,
∴DE⊥AC,
∵OA=OB,BD=CD,
∴OD为△ABC的中位线,
∴OD∥AC,
∴OD⊥DE,
∴DE为⊙O的切线.

【点评】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了圆周角定理和等腰三角形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



 B.
B.



 有意义,则x的取值是( )
有意义,则x的取值是( )