题目内容
如图,根据图形填空:
已知:AB∥DE,求∠B+∠BCD+∠D的度数.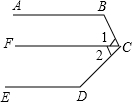
解:过点C画FC∥AB
∴∠B+∠1=180°(________),
∵AB∥DE(________)
FC∥AB(作图)
∴FC∥DE (________)
∴∠D+∠2=180°
∴∠B+∠1+∠D+∠2=360°(等式的性质)
即:∠B+∠BCD+∠D=360°.
两直线平行,同旁内角互补 已知 如果两条直线都和第三条直线平行,那么这两条直线平行
分析:根据平行线的性质和平行线的判定填空.
解答:过点C画FC∥AB,
∴∠B+∠1=180°( 两直线平行,同旁内角互补),
∵AB∥DE( 已知),FC∥AB(作图),
∴FC∥DE ( 如果两条直线都和第三条直线平行,那么这两条直线平行),
∴∠D+∠2=180°,
∴∠B+∠1+∠D+∠2=360°(等式的性质),
即:∠B+∠BCD+∠D=360°.
点评:本题主要考查证明过程中理论依据的填写,训练学生证明步骤的书写,比较简单.
分析:根据平行线的性质和平行线的判定填空.
解答:过点C画FC∥AB,
∴∠B+∠1=180°( 两直线平行,同旁内角互补),
∵AB∥DE( 已知),FC∥AB(作图),
∴FC∥DE ( 如果两条直线都和第三条直线平行,那么这两条直线平行),
∴∠D+∠2=180°,
∴∠B+∠1+∠D+∠2=360°(等式的性质),
即:∠B+∠BCD+∠D=360°.
点评:本题主要考查证明过程中理论依据的填写,训练学生证明步骤的书写,比较简单.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 15、如图,根据图形填空
15、如图,根据图形填空 如图,根据图形填空:
如图,根据图形填空: 24、如图,根据图形填空:
24、如图,根据图形填空: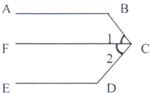 29、如图,根据图形填空:
29、如图,根据图形填空:
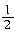 ∠( );
∠( ); ( );
( );