题目内容
求所有的实数m,使得关于x的方程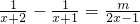 有且只有整数根.
有且只有整数根.
解:由题意,得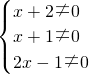 ,
,
解得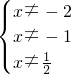 ;
;
又由原方程,得
mx2+(3m+2)x+2m-1=0 ①
当m=0时,x= ,不合题意(因为分母2x-1≠0);
,不合题意(因为分母2x-1≠0);
当m≠0时,设x1、x2(x1≤x2)是方程①的两个整数根,由韦达定理,得
x1+x2=-3- ②
②
x1•x2=2- ③
③
由②③消去m,得
(2x1-1)(2x2-1)=15,
∴(1)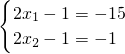 ,(2)
,(2)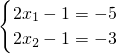 ,(3)
,(3)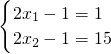 ,(4)
,(4)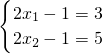 ,
,
解得(1)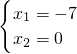 ,(2)
,(2)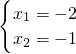 (舍去),(3)
(舍去),(3)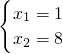 ,(4)
,(4)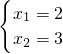
从而得m= ,m=
,m= ,m=
,m= .
.
分析:根据分式的性质(分母不为0)确定未知数x的取值范围;然后由根与系数的关系求得原方程的所有根;最后,将所有的整数根代入原方程并求得实数m的值.
点评:本题主要考查的是如何解分式方程:
(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.
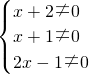 ,
,解得
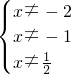 ;
;又由原方程,得
mx2+(3m+2)x+2m-1=0 ①
当m=0时,x=
 ,不合题意(因为分母2x-1≠0);
,不合题意(因为分母2x-1≠0);当m≠0时,设x1、x2(x1≤x2)是方程①的两个整数根,由韦达定理,得
x1+x2=-3-
 ②
②x1•x2=2-
 ③
③由②③消去m,得
(2x1-1)(2x2-1)=15,
∴(1)
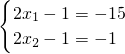 ,(2)
,(2)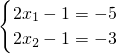 ,(3)
,(3)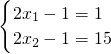 ,(4)
,(4)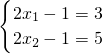 ,
,解得(1)
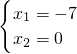 ,(2)
,(2)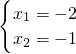 (舍去),(3)
(舍去),(3)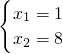 ,(4)
,(4)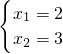
从而得m=
 ,m=
,m= ,m=
,m= .
.分析:根据分式的性质(分母不为0)确定未知数x的取值范围;然后由根与系数的关系求得原方程的所有根;最后,将所有的整数根代入原方程并求得实数m的值.
点评:本题主要考查的是如何解分式方程:
(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.

练习册系列答案
相关题目
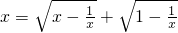 .
.