题目内容
在矩形ABCD中,AB=4,AD=3,P是AB上一动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为
- A.2.4
- B.2.5
- C.5
- D.4.8
A
分析:先连接DP、CP,根据三角形面积公式可知S△APC= AP×BC=
AP×BC= AC×PE,S△BPD=
AC×PE,S△BPD= BP×BC=
BP×BC= BD×PF,而AC=BD,利用勾股定理又可求AC=5,从而易求S△APC+S△BPD=
BD×PF,而AC=BD,利用勾股定理又可求AC=5,从而易求S△APC+S△BPD= (AP+BP)×BC=
(AP+BP)×BC= AB×BC=
AB×BC= AC×(PE+PF),也就可计算PE+PF.
AC×(PE+PF),也就可计算PE+PF.
解答: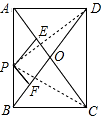 解:如右图所示,连接DP、CP,
解:如右图所示,连接DP、CP,
∵S△APC= AP×BC=
AP×BC= AC×PE,
AC×PE,
S△BPD= BP×BC=
BP×BC= BD×PF,
BD×PF,
又∵四边形ABCD是矩形,
∴AC=BD,
∴S△APC+S△BPD= (AP+BP)×BC=
(AP+BP)×BC= AB×BC=
AB×BC= AC×(PE+PF),
AC×(PE+PF),
在Rt△ABC中,AB=4,BC=3,
∴AC= =5,
=5,
∴ ×3×4=
×3×4= ×5×(PE+PF),
×5×(PE+PF),
∴PE+PF=2.4.
故选A.
点评:本题考查了矩形的性质、三角形的面积公式、勾股定理.解题的关键是证明S△APC+S△BPD= (AP+BP)×BC=
(AP+BP)×BC= AB×BC=
AB×BC= AC×(PE+PF).
AC×(PE+PF).
分析:先连接DP、CP,根据三角形面积公式可知S△APC=
 AP×BC=
AP×BC= AC×PE,S△BPD=
AC×PE,S△BPD= BP×BC=
BP×BC= BD×PF,而AC=BD,利用勾股定理又可求AC=5,从而易求S△APC+S△BPD=
BD×PF,而AC=BD,利用勾股定理又可求AC=5,从而易求S△APC+S△BPD= (AP+BP)×BC=
(AP+BP)×BC= AB×BC=
AB×BC= AC×(PE+PF),也就可计算PE+PF.
AC×(PE+PF),也就可计算PE+PF.解答:
 解:如右图所示,连接DP、CP,
解:如右图所示,连接DP、CP,∵S△APC=
 AP×BC=
AP×BC= AC×PE,
AC×PE,S△BPD=
 BP×BC=
BP×BC= BD×PF,
BD×PF,又∵四边形ABCD是矩形,
∴AC=BD,
∴S△APC+S△BPD=
 (AP+BP)×BC=
(AP+BP)×BC= AB×BC=
AB×BC= AC×(PE+PF),
AC×(PE+PF),在Rt△ABC中,AB=4,BC=3,
∴AC=
 =5,
=5,∴
 ×3×4=
×3×4= ×5×(PE+PF),
×5×(PE+PF),∴PE+PF=2.4.
故选A.
点评:本题考查了矩形的性质、三角形的面积公式、勾股定理.解题的关键是证明S△APC+S△BPD=
 (AP+BP)×BC=
(AP+BP)×BC= AB×BC=
AB×BC= AC×(PE+PF).
AC×(PE+PF). 
练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 7、如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,AE=5,则AD等于( )
7、如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,AE=5,则AD等于( ) 如图,在矩形ABCD中,AB=4,BC=7,P是BC边上与B点不重合的动点,过点P的直线交CD的延长线于R,交AD于Q(Q与D不重合),且∠RPC=45°,设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系,并求自变量x的取值范围.
如图,在矩形ABCD中,AB=4,BC=7,P是BC边上与B点不重合的动点,过点P的直线交CD的延长线于R,交AD于Q(Q与D不重合),且∠RPC=45°,设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系,并求自变量x的取值范围. 如图,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.求证:AE=BF.
如图,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.求证:AE=BF. 在矩形ABCD中,AB=8,AD=6,E为AB边上一点,连接DE,过C作CF垂直DE.
在矩形ABCD中,AB=8,AD=6,E为AB边上一点,连接DE,过C作CF垂直DE. 如图,在矩形ABCD中,AF、BE、CE、DF分别是矩形的四个角的角平分线,E、M、F、N是其交点,求证:四边形EMFN是正方形.
如图,在矩形ABCD中,AF、BE、CE、DF分别是矩形的四个角的角平分线,E、M、F、N是其交点,求证:四边形EMFN是正方形.