题目内容
已知正方形ABCD边长为1cm，点E在对角线BD上，BE=BC，P是CE上一动点，PF⊥BD，PG⊥BC，PF+PG的值为________．
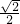
分析：连接BP，PF、PG分别为△BPE和△BCP的高，且底边长均为1，因此根据面积计算方法即可以求PF+PG．
解答：
解：连接BP，作EH⊥BC，则PF、PG分别为△BPE和△BCP的高，且底边长均为1，S△BCE=1-
-S△CDE，∵DE=BD-BE=
，△CDE中CD边上的高为
（），∵S△CDE=CD×
（）=-
；S△BCE=1-
-S△CDE=；又∵S△BCE=S△BPE+S△BPC=
•BC•（PF+PG）∴PF+PG=
=．故答案为：
．点评：本题考查了用求三角形面积的方法求三角形的高的转化思想，正方形对角线互相垂直且对角线即角平分线的性质，面积转换思想是解决本题的关键．
练习册系列答案
相关题目
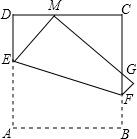折痕交AD于E，交BC于F，边AB折叠后与BC边交于点G．设点M的运动时间为t（0＜t＜10），单位：s．
已知正方形ABCD边长为1cm，点E在对角线BD上，BE=BC，P是CE上一动点，PF⊥BD，PG⊥BC，PF+PG的值为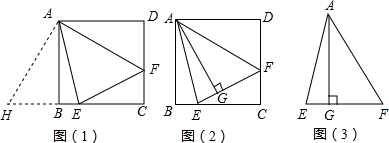
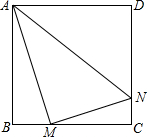如图所示，已知正方形ABCD边长为4，点M、N分别在边BC、CD上（点M、N都不与点B、C、D重合），且AM⊥MN．