题目内容
已知正方形ABCD边长为8CM,将该正方形在一直线上按顺时针方向沿着边滚动,每秒转动90°,转动3秒后停止,则顶点A经过的路线长为分析:正方形在一直线上按顺时针方向沿着边滚动,每秒转动90°,转动3秒钟,顶点A经过的路线有两种情况:一种是由两条弧构成,一条是圆心角为90°,半径为8CM,另一条是圆心角为90°,半径为8
CM.第二种是由三条弧构成,其中两条的圆心角是90°,半径为8CM,另一条的圆心角是90°,半径是8
CM.然后利用弧长公式求出点A经过的路线的长.
| 2 |
| 2 |
解答:解:第一种:
+
=4π+4
π(CM)
第二种:
×2+
=8π+4
π(CM)
故答案是:4π+4
πCM 或8π+4
πCM.
| 90•π•8 |
| 180 |
90•π•8
| ||
| 180 |
| 2 |
第二种:
| 90•π•8 |
| 180 |
90•π•8
| ||
| 180 |
| 2 |
故答案是:4π+4
| 2 |
| 2 |
点评:本题考查的是弧长的计算,根据题意得到点A经过的路线是两条或者三条弧,分析弧所对圆心角的度数和弧的半径,利用弧长公式求出点A经过的路线的长.

练习册系列答案
相关题目
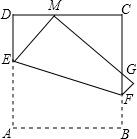 折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.设点M的运动时间为t(0<t<10),单位:s.
折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.设点M的运动时间为t(0<t<10),单位:s. 已知正方形ABCD边长为1cm,点E在对角线BD上,BE=BC,P是CE上一动点,PF⊥BD,PG⊥BC,PF+PG的值为
已知正方形ABCD边长为1cm,点E在对角线BD上,BE=BC,P是CE上一动点,PF⊥BD,PG⊥BC,PF+PG的值为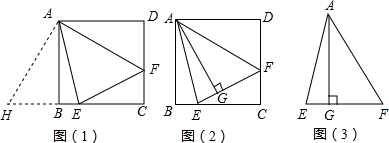
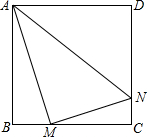 如图所示,已知正方形ABCD边长为4,点M、N分别在边BC、CD上(点M、N都不与点B、C、D重合),且AM⊥MN.
如图所示,已知正方形ABCD边长为4,点M、N分别在边BC、CD上(点M、N都不与点B、C、D重合),且AM⊥MN.