题目内容
 (2013•溧水县一模)如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是
(2013•溧水县一模)如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是4
| 2 |
4
cm.| 2 |
分析:先利用弧长公式得到圆心角为120°,半径为6cm的扇形的弧长=4π,根据圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长,则可计算出圆锥的底面圆的半径为2,然后根据勾股定理可计算出圆锥的高.
解答:解:∵圆心角为120°,半径为6cm的扇形的弧长=
=4π,
∴圆锥的底面圆的周长为4π,
∴圆锥的底面圆的半径为2,
∴这个纸帽的高=
=4
(cm).
故答案为4
.
| 120•π•6 |
| 180 |
∴圆锥的底面圆的周长为4π,
∴圆锥的底面圆的半径为2,
∴这个纸帽的高=
| 62-22 |
| 2 |
故答案为4
| 2 |
点评:本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长,扇形的半径等于圆锥的母线长.也考查了弧长公式和勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
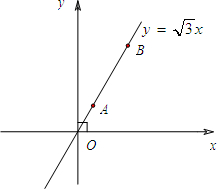 (2013•溧水县一模)如图,在平面直角坐标系中,A、B为正比例函数
(2013•溧水县一模)如图,在平面直角坐标系中,A、B为正比例函数