Question

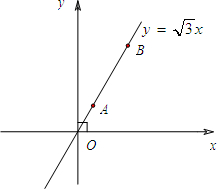（2013•溧水县一模）如图，在平面直角坐标系中，A、B为正比例函数y=

3

x图象上的两点，且OB=2，AB=

2

．点P在y轴上，△BPA是以∠B为顶角的等腰三角形，则OP的长为

3

+1或

3

-1

．

Answer 1

分析：根据B为正比例函数y=

3

x图象上的点，且OB=2，求出B点的坐标，设P点坐标为（0，a），由题意，△BPA是以∠B为顶角的等腰三角形，则BP=PA，列出关于a的一元二次方程，求出a的值，OP的长即可求出．

解答：解：设B点的坐标为（m，n），
∵B为正比例函数y=

3

x图象上的点，且OB=2，
∴

n= 3 m m2+n2=4

，
解得：

m=1 n= 3

或

m=-1 n=- 3

（舍去），
∴点B的坐标为（1，

3

），
设P点坐标为（0，a），由题意，
∵△BPA是以∠B为顶角的等腰三角形，
∴BP=PA，
∴

(a- 3 )2+1

=|AB|=

2

，
整理得（a-

3

）²=1，
解得a=

3

+1或

3

-1，
则OP的长为

3

+1或

3

-1，
故答案为

3

+1或

3

-1．

点评：本题主要考查一次函数的综合题，解答本题的关键是求出B点的坐标，解答此题还要注意△BPA是以∠B为顶角的等腰三角形，此题容易出现错误，希望同学们审题时候要注意．