题目内容
 已知:如图,正八边形A1A2A3A4A5A6A7A8内接于半径为R的⊙O.
已知:如图,正八边形A1A2A3A4A5A6A7A8内接于半径为R的⊙O.(1)求A1A3的长;
(2)求四边形A1A2A3O的面积;
(3)求此正八边形的面积S.
分析:(1)根据正多边形中心角求法得出∠A3OA2=∠A2OA1=
=45°,进而得出∠A3OA1=90°,再利用勾股定理求出A3A1;
(2)利用已知得出OA2⊥A1A3,得出四边形A1A2A3O的面积为:
OA2•A3B+
OA2•A1B进而求出即可;
(3)利用(2)中所求即可得出正八边形的面积S为:
×
R2得出答案即可.
| 360° |
| 8 |
(2)利用已知得出OA2⊥A1A3,得出四边形A1A2A3O的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
(3)利用(2)中所求即可得出正八边形的面积S为:
| 360 |
| 90 |
| ||
| 2 |
解答: 解:(1)∵正八边形A1A2A3A4A5A6A7A8内接于半径为R的⊙O.
解:(1)∵正八边形A1A2A3A4A5A6A7A8内接于半径为R的⊙O.
∴∠A3OA2=∠A2OA1=
=45°,
∴∠A3OA1=90°,
∵OA3=OA1=R,
∴A3A1=
=
=
R;
(2)∵∠A3OA2=∠A2OA1=45°,
∴
=
,
∴OA2⊥A1A3,
四边形A1A2A3O的面积为:
OA2•A3B+
OA2•A1B=
OA2•A1A3=
R•
R=
R2;
(3)∵四边形A1A2A3O的面积为:
R2,∠A3OA1=90°,
∴正八边形的面积S为:
×
R2=2
R2.
 解:(1)∵正八边形A1A2A3A4A5A6A7A8内接于半径为R的⊙O.
解:(1)∵正八边形A1A2A3A4A5A6A7A8内接于半径为R的⊙O.∴∠A3OA2=∠A2OA1=
| 360° |
| 8 |
∴∠A3OA1=90°,
∵OA3=OA1=R,
∴A3A1=
O
|
| 2R2 |
| 2 |
(2)∵∠A3OA2=∠A2OA1=45°,
∴
 |
| A3A2 |
 |
| A2A1 |
∴OA2⊥A1A3,
四边形A1A2A3O的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
(3)∵四边形A1A2A3O的面积为:
| ||
| 2 |
∴正八边形的面积S为:
| 360 |
| 90 |
| ||
| 2 |
| 2 |
点评:此题主要考查了正多边形和圆的有关计算,根据已知得出中心角∠A3OA1=90°再利用勾股定理得出是解题关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目



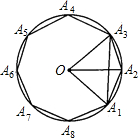 已知:如图,正八边形A1A2A3A4A5A6A7A8内接于半径为R的⊙O.
已知:如图,正八边形A1A2A3A4A5A6A7A8内接于半径为R的⊙O.