题目内容
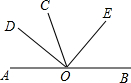 如图,O是直线AB上的点,OD是∠AOC的平分线,OE是∠COB的平分线,求∠DOE的度数.
如图,O是直线AB上的点,OD是∠AOC的平分线,OE是∠COB的平分线,求∠DOE的度数.(1)一变:如图,∠DOE=90°,OD平分∠AOC,问OE是否平分∠BOC?
(2)二变:如图,点O在直线AB上,且∠AOC≠∠BOC,OD平分∠AOC,∠DOE=90°,下面四个结论,错误的有( )
①图中必有3个钝角;②图中只有3对既相邻又互补的角;③图中没有45°的角;④OE是∠BOC的平分线.
A.0个;B.1个;C.2个;D.3个.
分析:根据OD是∠AOC的平分线,OE是∠COB的平分线,又知∠AOC+∠BOC=180°,故可得∠DOE的度数.
(1)由∠AOC+∠BOC=180°,∠DOE=90°,可得∠DOE=
(∠AOC+∠BOC),进而得到∠COE=
∠BOC.
(2)根据∠AOC≠∠BOC,OD平分∠AOC,∠DOE=90°,再结合图形进行判断.
(1)由∠AOC+∠BOC=180°,∠DOE=90°,可得∠DOE=
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据∠AOC≠∠BOC,OD平分∠AOC,∠DOE=90°,再结合图形进行判断.
解答:解:由题意可知∠DOC=
∠AOC,∠EOC=
∠BOC.
因为AB是一条直线,所以∠AOB=180°,也就是∠AOC+∠BOC=180°,∠DOE=∠DOC+∠EOC=
∠AOC+
∠BOC=90°.
(1)解:∵∠AOC+∠BOC=180°,∠DOE=90°,
∴∠DOE=
(∠AOC+∠BOC)=
∠AOC+
∠BOC,
而∠DOE=∠DOC+∠EOC,∠DOC=
∠AOC,
∴∠COE=
∠BOC,即OE平分∠BOC.
(2)∵∠AOC≠∠BOC,OD平分∠AOC,∠DOE=90°,
∴图中必有3个钝角;图中只有3对既相邻又互补的角;图中没有45°的角;OE是∠BOC的平分线.
故选A.
| 1 |
| 2 |
| 1 |
| 2 |
因为AB是一条直线,所以∠AOB=180°,也就是∠AOC+∠BOC=180°,∠DOE=∠DOC+∠EOC=
| 1 |
| 2 |
| 1 |
| 2 |
(1)解:∵∠AOC+∠BOC=180°,∠DOE=90°,
∴∠DOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
而∠DOE=∠DOC+∠EOC,∠DOC=
| 1 |
| 2 |
∴∠COE=
| 1 |
| 2 |
(2)∵∠AOC≠∠BOC,OD平分∠AOC,∠DOE=90°,
∴图中必有3个钝角;图中只有3对既相邻又互补的角;图中没有45°的角;OE是∠BOC的平分线.
故选A.
点评:本题考查角与角之间的运算,注意结合图形,发现角与角之间的关系,进而求解.

练习册系列答案
相关题目
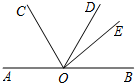 如图,O是直线AB上一点,OC,OD,OE是三条射线,且OC平分∠AOD,∠BOE=2∠DOE,∠COE=80°,求∠BOE的度数.
如图,O是直线AB上一点,OC,OD,OE是三条射线,且OC平分∠AOD,∠BOE=2∠DOE,∠COE=80°,求∠BOE的度数.
 如图,O是直线AB上一点,∠AOC=134°18′,求∠BOC的度数.
如图,O是直线AB上一点,∠AOC=134°18′,求∠BOC的度数. 如图,O是直线AB上的一点,∠AOC=53°17′,则∠BOC的度数是
如图,O是直线AB上的一点,∠AOC=53°17′,则∠BOC的度数是 如图,O是直线AB上任意一点,OC平分∠AOB.按下列要求画图并回答问题:
如图,O是直线AB上任意一点,OC平分∠AOB.按下列要求画图并回答问题: