题目内容
10.在△ABC中,∠C=90°,AC=3,BC=4,△ABC外接圆⊙O的半径为2.5,△ABC内切圆⊙I的半径为1.分析 由勾股定理求出斜边AB,直角三角形外接圆的半径等于斜边的一半,即可得出△ABC外接圆⊙O的半径.由切线长定理得出AE=AD,CE=CF,BD=BF;证出四边形IECF是正方形,则列方程即可求得⊙I的半径r.
解答 解:∵∠C=90°,AC=3,BC=4,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴△ABC外接圆的半径为$\frac{1}{2}$AB=2.5;
连接△ABC内切圆⊙I的圆心I和各个切点,如图所示.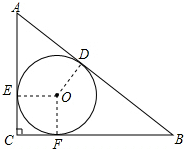
∵⊙I为△ABC的内切圆,
∴AE=AD,CE=CF,BD=BF,IE⊥AC,IF⊥BC,
∴∠IFC=∠IEC=∠C=90°,
∴四边形IECF是矩形;
∵IE=IF,
∴四边形IECF是正方形;
∵⊙I的半径为r,
∴CE=CF=r,AE=AD=3-r,BD=BF=4-r,
∴3-r+4-r=5,
解得:r=1,
∴△ABC的内切圆的半径r=1.
故答案为:2.5,1.
点评 本题考查了直角三角形外接圆和内切圆的性质、切线长定理、勾股定理、正方形的判定;熟知直角三角形外接圆的半径等于斜边的一半和由勾股定理求出内切圆半径是解决问题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
1.白浪河是潍坊的母亲河,为打造特色滨水景观区,现有一段河道整治任务由A、B两工程队完成.A工程队单独整治该河道要16天才能完成;B工程队单独整治该河道要24天才能完成.现在A工程队单独做6天后,B工程队加入合做完成剩下的工程,那么A工程队一共做的天数是( )
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
18.下列各式从左到右的变形属于分解因式的是( )
| A. | (m-2)(m-3)=(2-m)(3-m) | B. | x2-4x+4=(x-2)2 | C. | (x+1)(x-1)=x2-1 | D. | a2-2a+3=(a-1)2+2 |
15.某玩具的标价是132元,若降价以9折出售仍可获利10%,则该玩具的进价是( )元.
| A. | 118 | B. | 108 | C. | 106 | D. | 105 |
2. 如图是甲、乙两家公司衬衫销售情况的统计图,由该图可以判断( )
如图是甲、乙两家公司衬衫销售情况的统计图,由该图可以判断( )
 如图是甲、乙两家公司衬衫销售情况的统计图,由该图可以判断( )
如图是甲、乙两家公司衬衫销售情况的统计图,由该图可以判断( )| A. | 甲公司销售量多 | B. | 乙公司销售量多 | ||
| C. | 两家销售量一样多 | D. | 不能判断 |
19.已知x2+y2=25,xy=12,那么x2-y2=( )
| A. | 7 | B. | ±7 | C. | -7 | D. | 以上都不是 |
 如图,已知AB=AE,AC=AD,增加下列条件:①∠CAE=∠DAB;②BC=ED;③∠C=∠D=90°;④∠B=∠E.其中能使△ABC≌△AED的条件有( )
如图,已知AB=AE,AC=AD,增加下列条件:①∠CAE=∠DAB;②BC=ED;③∠C=∠D=90°;④∠B=∠E.其中能使△ABC≌△AED的条件有( )