题目内容
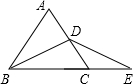在等边△ABC中，D为AC的中点，E为BC延长线上一点，且DB=DE，若△ABC的周长为12，则△DCE的周长为（ ）| A、4 | ||
B、4+2
| ||
C、4+
| ||
D、4+2
|
分析：根据等边三角形的性质，先求出DE=DB=2
，再证CE=CD=2，从而得△DCE的周长为4+2
．
| 3 |
| 3 |
解答：解：∵△ABC是等边三角形，且D是AC边的中点，
∴BD⊥AC，∠CBD=∠ABD=30°，AB=BC=AC=4
∵BD=DE
∴∠DBC=∠E=30°
∴∠BDE=180°-30°-30°=120°
∵∠BDC=90°
∴∠CDE=∠E=30°
∴CD=CE=
AC=2
直角三角形BCD中，BD=
=
=2
∴DE=BD=2
∴三角形DCE的周长=DC+DE+CE=4+2
．
故选B．
∴BD⊥AC，∠CBD=∠ABD=30°，AB=BC=AC=4
∵BD=DE
∴∠DBC=∠E=30°
∴∠BDE=180°-30°-30°=120°
∵∠BDC=90°
∴∠CDE=∠E=30°
∴CD=CE=
| 1 |
| 2 |
直角三角形BCD中，BD=
| BC2-CD2 |
| 42-22 |
| 3 |
∴DE=BD=2
| 3 |
∴三角形DCE的周长=DC+DE+CE=4+2
| 3 |
故选B．
点评：本题综合考查等腰三角形与等边三角形的性质，勾股定理及三角形内角和为180°等知识．
练习册系列答案
相关题目
15、如图，在等边△ABC中，D、E分别是AB、AC上的点，且AD=CE，则∠BCD+∠CBE=
如图，在等边△ABC中，AC=8，点O在AC上，且AO=3，点P是AB上一动点，连接OP，将线段OP绕点O逆时针旋转60°得到线段OD．要使点D恰好落在BC上，则AP的长是
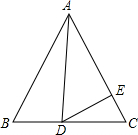如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADE=60°，BD=3，CE=2，则△ABC的面积为（ ）A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
如图在等边△ABC中，P是BC边上一点，D为AC上一点，且∠APD=60°，BP=3，CD=2，则△CPD，△BAP，△APD的面积比为