题目内容
11．已知关于x的方程x2+px+q=0的两根为-3和-1，则p=4，q=3．分析 由根与系数的关系可得出关于p或q的一元一次方程，解之即可得出结论．
解答 解：∵关于x的方程x2+px+q=0的两根为-3和-1，
∴-3+（-1）=-p，（-3）×（-1）=q，
∴p=4，q=3．
故答案为：4；3．
点评 本题考查了根与系数的关系，根据根与系数的关系找出-3+（-1）=-p、（-3）×（-1）=q是解题的关键．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
1．已知抛物线y=x2-4x+3与x轴相交于点A，B（点A在点B左侧），顶点为M．平移该抛物线，使点M平移后的对应点M'落在x轴上，点B平移后的对应点B'落在y轴上，则平移后的抛物线解析式为（ ）
| A． | y=x2+2x+1 | B． | y=x2+2x-1 | C． | y=x2-2x+1 | D． | y=x2-2x-1 |
2．
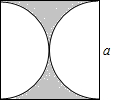如图所示，边长为a的正方形中阴影部分的面积为（ ）
如图所示，边长为a的正方形中阴影部分的面积为（ ）| A． | a2-π（$\frac{a}{2}$）2 | B． | a2-πa2 | C． | a2-πa | D． | a2-2πa |
6．
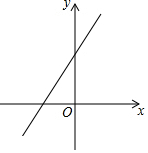在平面直角坐标系中，一次函数y=kx+b的图象如图所示，观察图象可得（ ）
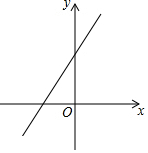在平面直角坐标系中，一次函数y=kx+b的图象如图所示，观察图象可得（ ）| A． | k＞0，b＞0 | B． | k＞0，b＜0 | C． | k＜0，b＞0 | D． | k＜0，b＜0 |
16．某公司共25名员工，下表是他们月收入的资料．
（1）该公司员工月收入的中位数是3400元，众数是3000元．
（2）根据上表，可以算得该公司员工月收入的平均数为6276元．你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适？说明理由．
| 月收入/元 | 45000 | 18000 | 10000 | 5500 | 4800 | 3400 | 3000 | 2200 |
| 人数 | 1 | 1 | 1 | 3 | 6 | 1 | 11 | 1 |
（2）根据上表，可以算得该公司员工月收入的平均数为6276元．你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适？说明理由．
3．
如图示直线l1，l2△ABC被直线l3所截，且l1∥l2，则α=（ ）
如图示直线l1，l2△ABC被直线l3所截，且l1∥l2，则α=（ ）| A． | 41° | B． | 49° | C． | 51° | D． | 59° |
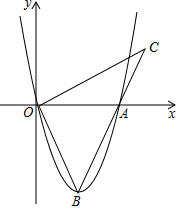如图，抛物线y=ax2-4x的图象与x轴的一个交点为A（6，0），点B为抛物线的顶点，连结OB、AB，作OC⊥OB交BA的延长线于点C．