题目内容
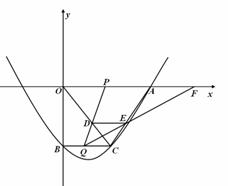
如图,射线 于点
于点 ,点
,点 、
、 在
在 上,
上, 为线段
为线段 的中点,且
的中点,且 于
于 点.
点.

(1)若 ,△
,△ 的面积为
的面积为 .
.
①直接写出 的值;
的值;
②求△ 的周长;
的周长;
(2)若 ,
, 点在射线
点在射线 上移动,问此过程中,
上移动,问此过程中, 的值是否会为定值?若会,请求出这个定值;若不会,请求出它的取值范围.
的值是否会为定值?若会,请求出这个定值;若不会,请求出它的取值范围.
【答案】
(1)① ;②
;② ;(2)定值
;(2)定值
【解析】
试题分析:(1)①根据勾股定理即可求得结果;
②根据直角三角形的面积公式可得 ,即可得
,即可得 ,再有
,再有 可得到
可得到 ,可得
,可得 ,从而可以求得结果;
,从而可以求得结果;
(2)连结 ,在Rt△
,在Rt△ 中,根据勾股定理可得
中,根据勾股定理可得 ,在Rt△
,在Rt△ 中,根据勾股定理可得
中,根据勾股定理可得 ,再结合
,再结合 可得
可得 ,在Rt△
,在Rt△ 中,根据勾股定理可得
中,根据勾股定理可得 =
= ,从而可以得到
,从而可以得到 是一个定值.
是一个定值.
(1)① ;
;
②∵
∴△ 是直角三角形
是直角三角形
∵△ 的面积为
的面积为 ,
,
∴ ,即
,即
由①可知:
∴
∴
∵
∴
∴ ,即△
,即△ 的周长为
的周长为 ;
;
(2)连结
在Rt△ 中,
中, ……①
……①
在Rt△ 中,
中, ……②
……②
∴ 得:
得:
∵
∴
在Rt△ 中,
中, =
=
∴
故在点 移动过程中,
移动过程中, 的值是定值,其值是
的值是定值,其值是 .
.
考点:勾股定理的应用
点评:解答本题上的根据是读懂题意及图形,选择恰当的直角三角形熟练掌握勾股定理解题.

练习册系列答案
相关题目
 于点
于点 ,点
,点 、
、 在
在 上,
上, 为线段
为线段 的中点,且
的中点,且 于
于 点.
点.
 ,△
,△ 的面积为
的面积为 .
. 的值;
的值; ,
, 上移动,问此过程中,
上移动,问此过程中, 的值是否会为定值?若会,请求出这个定值;若不会,请求出它的取值范围.
的值是否会为定值?若会,请求出这个定值;若不会,请求出它的取值范围. x2+3与x轴交于点A,点B,与直线y=
x2+3与x轴交于点A,点B,与直线y= x+b相交于点B,点C,直线y=
x+b相交于点B,点C,直线y= x+b与y轴交于点E.
x+b与y轴交于点E.