题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 为半径作半圆,交
为半径作半圆,交![]() 于点
于点![]() .
.
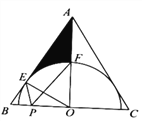
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若点![]() 是
是![]() 的中点,
的中点,![]() ,求图中阴影部分的面积;
,求图中阴影部分的面积;
(3)在(2)的条件下,点![]() 是
是![]() 边上的动点,当
边上的动点,当![]() 取最小值时,直接写出
取最小值时,直接写出![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)过![]() 作
作![]() 垂线
垂线![]() ,垂足为
,垂足为![]() ,证明OM=OE即可;
,证明OM=OE即可;
(2)根据“S△AEO-S扇形EOF=S阴影”进行计算即可;
(3)作![]() 关于
关于![]() 的对称点
的对称点![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,此时
,此时![]() 最小.通过证明
最小.通过证明![]() ∽
∽![]() 即可求解
即可求解
(1)过![]() 作
作![]() 垂线
垂线![]() ,垂足为
,垂足为![]()

∵![]() ,
,![]()
∴![]() 平分
平分![]()
∵![]()
∴![]()
∵![]() 为⊙
为⊙![]() 的半径,
的半径,
∴![]() 为⊙
为⊙![]() 的半径,
的半径,
∴![]() 是⊙
是⊙![]() 的切线
的切线
(2)∵![]() 且
且![]() 是
是![]() 的中点
的中点
∴![]() ,
,![]() ,
,
∴![]()
∵![]()
∴![]() 即
即![]() ,
,
∴![]()
(3)作![]() 关于
关于![]() 的对称点
的对称点![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]()
此时![]() 最小
最小
由(2)知![]() ,
,![]() ,
,
∴![]()
∵![]()
∴![]() ,
,![]() ,
,![]()
∵![]() ,
,![]()
∴![]() ∽
∽![]()
∴![]() 即
即![]()
∵![]() ,
,
∴![]() 即
即![]() ,
,
∴![]() .
.

练习册系列答案
相关题目