题目内容
在四边形ABCD中,AB=3,AD=4,∠BCD=120°,AB⊥BC,AD⊥DC,则BD=________,AC=________.


分析:根据四边形的内角和定理求出∠BAD=60°,然后在△ABD中由余弦定理求得BD的值;
由已知条件AB⊥BC,AD⊥DC推知AC是四边形ABCD外接圆直径,AC也是△ABD外接圆直径,然后利用正弦定理求出AC的长度即可.
解答:
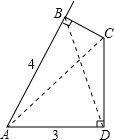 解:如图,∠BAD=180°-120°=60°,
解:如图,∠BAD=180°-120°=60°,由余弦定理,知
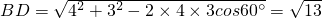 ,
,∵AB⊥BC,AD⊥DC,
∴AC是四边形ABCD外接圆直径,
∴AC也是△ABD外接圆直径,由正弦定理得
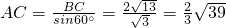 ,
,故答案为:
 .
.点评:本题主要考查了正弦定理与余弦定理及圆心角、弧、弦的关系.解答此题的难点是求出AC的长度,在解答AC的长度时,要灵活运用正弦定理:
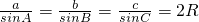 .
. 
练习册系列答案
相关题目
 11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
 如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?
如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?