题目内容
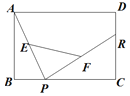
如图,矩形ABCD中R、P分别是DC、BC边上的点,AD=8,AB=6,CR=2DR,E、F分别是AP、RP的中点,当P在BC上从B向C移动而R不动时,线段EF长为_________.
练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
题目内容
如图,矩形ABCD中R、P分别是DC、BC边上的点,AD=8,AB=6,CR=2DR,E、F分别是AP、RP的中点,当P在BC上从B向C移动而R不动时,线段EF长为_________.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案