题目内容
 如图,⊙O1与⊙O内切于点A,△ABC内接于⊙O,AB、AC分别交⊙O1于点E和F,BD切⊙O1于点D,且FD是⊙O1的直径,延长FE交BD于点H.
如图,⊙O1与⊙O内切于点A,△ABC内接于⊙O,AB、AC分别交⊙O1于点E和F,BD切⊙O1于点D,且FD是⊙O1的直径,延长FE交BD于点H.(1)求证:EF∥BC;
(2)若∠DBC=60°,
 ,求
,求 的值.
的值.
【答案】分析:(1)过点A作两圆的公切线MN,根据切割线定理可得出∠EFA=∠BCA,继而可证明结论EF∥BC;
(2)连接DE并延长交BC于点G,DH=4k,则HB=5k,DB=9k,根据∠DBC=60°利用解直角三角形的知识,可得出BG、DG的长度,然后表示出BE的长度,根据 =1-
=1- ,即可得出答案.
,即可得出答案.
解答:证明:(1)如图,过点A作两圆的公切线MN,
∵∠EFA=∠EAM,∠BCA=∠BAM,
∴∠EFA=∠BCA,
∴EF∥BC.

(2)由条件,不妨设DH=4k,
则HB=5k,DB=9k,
连接DE并延长交BC于点G,
∵DF为⊙O1的直径,
∴DE⊥HF,∠DEH=90°,
∵EF∥BC.
∴∠DGB=∠DEH=90°,
∴ =
= =
= ,
,
而∠DBG=60°,
∴BG= DB=
DB= k,DG=
k,DG= DB=
DB= k,
k,
∴EG= DG=
DG= k,
k,
在Rt△BGE中,BE2=BG2+EG2=39k2,
∵BD是⊙O1的切线,
∴BD2=BE•BA,
∴ =
= =
= =
= ,
,
∴ =1-
=1- =
= .
.
点评:本题属于圆的综合题,涉及了切割线定理、平行线的判定、勾股定理及切线的性质,考察的知识点较多,解答本题的关键是要求同学们熟练掌握所学的定理及性质,对于这样的综合性题目,除了要求我们仔细思考之外,更考察我们的灵活运用能力.
(2)连接DE并延长交BC于点G,DH=4k,则HB=5k,DB=9k,根据∠DBC=60°利用解直角三角形的知识,可得出BG、DG的长度,然后表示出BE的长度,根据
 =1-
=1- ,即可得出答案.
,即可得出答案.解答:证明:(1)如图,过点A作两圆的公切线MN,
∵∠EFA=∠EAM,∠BCA=∠BAM,
∴∠EFA=∠BCA,
∴EF∥BC.

(2)由条件,不妨设DH=4k,
则HB=5k,DB=9k,
连接DE并延长交BC于点G,
∵DF为⊙O1的直径,
∴DE⊥HF,∠DEH=90°,
∵EF∥BC.
∴∠DGB=∠DEH=90°,
∴
 =
= =
= ,
,而∠DBG=60°,
∴BG=
 DB=
DB= k,DG=
k,DG= DB=
DB= k,
k,∴EG=
 DG=
DG= k,
k,在Rt△BGE中,BE2=BG2+EG2=39k2,
∵BD是⊙O1的切线,
∴BD2=BE•BA,
∴
 =
= =
= =
= ,
,∴
 =1-
=1- =
= .
.点评:本题属于圆的综合题,涉及了切割线定理、平行线的判定、勾股定理及切线的性质,考察的知识点较多,解答本题的关键是要求同学们熟练掌握所学的定理及性质,对于这样的综合性题目,除了要求我们仔细思考之外,更考察我们的灵活运用能力.

练习册系列答案
相关题目

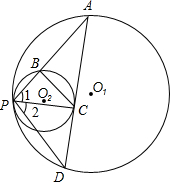 O1于D,且PB、PD的长恰好是关于x的方程
O1于D,且PB、PD的长恰好是关于x的方程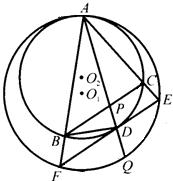 13、如图,⊙O1与⊙O2内切于点A,D为⊙O2上一点,过点D作⊙O2的切线交⊙O1于F、E,连接AF,AE,分别交⊙O2于B,C,连接BC,AD,BC与AD相交于点P,延长AD交⊙O1于Q.
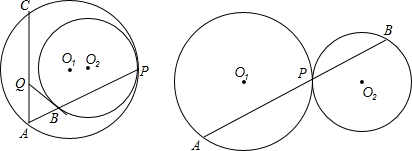
13、如图,⊙O1与⊙O2内切于点A,D为⊙O2上一点,过点D作⊙O2的切线交⊙O1于F、E,连接AF,AE,分别交⊙O2于B,C,连接BC,AD,BC与AD相交于点P,延长AD交⊙O1于Q. 如图,⊙O1与⊙O2内切于点A,其半径分别为r1与r2(r1>r2).若⊙O1的弦AB交⊙O2于点C(O1不在AB上),则AB:AC的值等于( )
如图,⊙O1与⊙O2内切于点A,其半径分别为r1与r2(r1>r2).若⊙O1的弦AB交⊙O2于点C(O1不在AB上),则AB:AC的值等于( )