题目内容
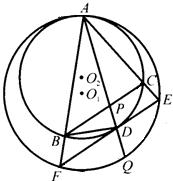 13、如图,⊙O1与⊙O2内切于点A,D为⊙O2上一点,过点D作⊙O2的切线交⊙O1于F、E,连接AF,AE,分别交⊙O2于B,C,连接BC,AD,BC与AD相交于点P,延长AD交⊙O1于Q.
13、如图,⊙O1与⊙O2内切于点A,D为⊙O2上一点,过点D作⊙O2的切线交⊙O1于F、E,连接AF,AE,分别交⊙O2于B,C,连接BC,AD,BC与AD相交于点P,延长AD交⊙O1于Q.(1)求证:BC∥EF;
(2)求证:FD•PC=AP•DQ.
分析:(1)如图过两圆的公切线MN,利用弦切角定理可以找到角的关系证明BC∥EF;
(2)利用平行线的性质和同弧上的圆周角相等可以找到证明△APC∽△FDQ的条件,然后利用相似三角形的性质就可以证明题目的结论.
(2)利用平行线的性质和同弧上的圆周角相等可以找到证明△APC∽△FDQ的条件,然后利用相似三角形的性质就可以证明题目的结论.
解答: 解:(1)如图过两圆的公切线MN,
解:(1)如图过两圆的公切线MN,
∵∠NAC=∠ABC=∠AFD,
∴BC∥EF.
(2)连接FQ,
∵BC∥EF,
∴∠ACP=∠AED,
∵∠AED=∠AQF,∠AQF=∠ACP,
又∵∠EAP=∠DFQ,
∴△APC∽△FDQ.
∴FD•PC=AP•DQ.
 解:(1)如图过两圆的公切线MN,
解:(1)如图过两圆的公切线MN,∵∠NAC=∠ABC=∠AFD,
∴BC∥EF.
(2)连接FQ,
∵BC∥EF,
∴∠ACP=∠AED,
∵∠AED=∠AQF,∠AQF=∠ACP,
又∵∠EAP=∠DFQ,
∴△APC∽△FDQ.
∴FD•PC=AP•DQ.
点评:熟练掌握弦切角定理和相似三角形的性质是解决问题的关键.

练习册系列答案
相关题目
 12、已知:如图,⊙O1与⊙O2外切于点P,直线AB过点P交⊙O1于A,交⊙O2于B,点C、D分别为⊙O1、⊙O2上的点,且∠ACP=65°,则∠BDP=
12、已知:如图,⊙O1与⊙O2外切于点P,直线AB过点P交⊙O1于A,交⊙O2于B,点C、D分别为⊙O1、⊙O2上的点,且∠ACP=65°,则∠BDP=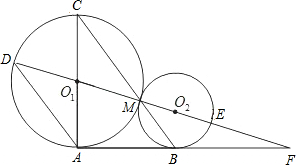 已知:如图,⊙O1与⊙O2外切于M点,AF是两圆的外公切线,A、B是切点,DF经过O1、O2,分别交⊙O1于D、⊙O2于E,AC是⊙O1的直径,BC经过M点,连接AD.
已知:如图,⊙O1与⊙O2外切于M点,AF是两圆的外公切线,A、B是切点,DF经过O1、O2,分别交⊙O1于D、⊙O2于E,AC是⊙O1的直径,BC经过M点,连接AD.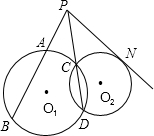 如图,⊙O1与⊙O2相交于C、D两点,⊙O1的割线PAB与DC的延长线交于点P,PN与⊙O2相切于点N,若PB=10,AB=6,则PN=
如图,⊙O1与⊙O2相交于C、D两点,⊙O1的割线PAB与DC的延长线交于点P,PN与⊙O2相切于点N,若PB=10,AB=6,则PN=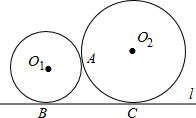 已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.
已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.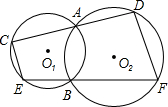 已知如图:⊙O1与⊙O2相交于AB两点,过点A、B的直线分别与⊙O1交于C、E,与⊙O2交于D、F,连接CE、DF.
已知如图:⊙O1与⊙O2相交于AB两点,过点A、B的直线分别与⊙O1交于C、E,与⊙O2交于D、F,连接CE、DF.