Question

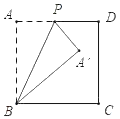
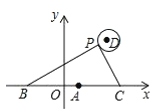
【题目】如图，在平面直角坐标系中，已知点A（1，0），B（1﹣a，0），C（1+a，0）（a＞0），点P在以D（4，4）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则a的最小值是_____．

Answer 1

【答案】4

【解析】

利用点A、B、C的坐标可得到AB=AC=a,则AB=AC=AP=a,连接AD交圆D于P',利用两点间的距离公式计算出DA=5,即可得到P'A=4,于是可判断a的最小值为4.

解:∵点A（1，0），B（1﹣a，0），C（1+a，0）（a＞0）,

∴AB=AC=a,
∵∠BPC=90°,

∴AB=AC=AP=a,
连接AD交圆D于P',
∴DA=5

∴P'A=5-1=4,
即圆D上点到A的最短距离为4,
∴a的最小值为4.
故答案为4.