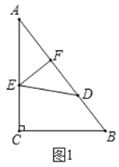
题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() ,
,![]() 上,连接
上,连接![]() .
.
(1)将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,如图1,若
处,如图1,若![]() ,求
,求![]() 的长;
的长;
(2)将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,如图2,若
处,如图2,若![]() .
.
①求![]() 的长;
的长;
②求四边形![]() 的面积;
的面积;
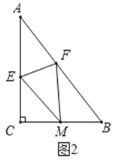
(3)若点![]() 在射线
在射线![]() 上,点
上,点![]() 在边
在边![]() 上,点
上,点![]() 关于
关于![]() 所在直线的对称点为点
所在直线的对称点为点![]() ,问:是否存在以
,问:是否存在以![]() 、
、![]() 为对边的平行四边形,若存在,求出
为对边的平行四边形,若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)存在,
;(3)存在,![]() 或6.
或6.
【解析】
(1)先判断出S△ABC=4S△AEF,再求出AB,判断出Rt△AEF∽△Rt△ABC,得出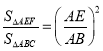 ,代值即可得出结论;
,代值即可得出结论;
(2)先判断出四边形AEMF是菱形,再判断出△CME∽△CBA得出比例式,代值即可得出结论;
(3)分两种情况,利用平行四边形的性质,对边平行且相等,最后用勾股定理即可得出结论.
解:(1)∵![]() 沿
沿![]() 折叠,折叠后点
折叠,折叠后点![]() 落在
落在![]() 上的点
上的点![]() 处,
处,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴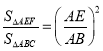 ,
,
即:![]() ,
,
∴![]() ;
;
(2)①∵![]() 沿
沿![]() 折叠,折叠后点
折叠,折叠后点![]() 落在
落在![]() 边上的点
边上的点![]() 处,
处,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是菱形,
是菱形,
设![]() ,则
,则![]() ,
,![]() ,
,
∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
即:![]() ,
,
②由①知,![]() ,
,![]() ,
,
∴![]() ;
;
(3)①如图3,当点![]() 在线段
在线段![]() 上时,
上时,
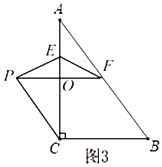
∵![]() 与
与![]() 是平行四边形的对边,
是平行四边形的对边,
∴![]() ,
,![]() ,
,
由对称性知,![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∴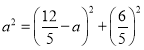 ,
,
∴![]() ,
,
即:![]() ;
;
②如图4,当点![]() 在线段
在线段![]() 的延长线上时,延长
的延长线上时,延长![]() 交
交![]() 于
于![]() ,
,
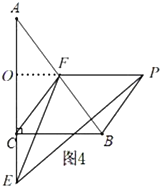
同理:![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∴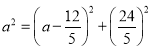 ,
,
∴![]() ,
,
∴![]() ,
,
即:![]() 或6.
或6.

 快捷英语周周练系列答案
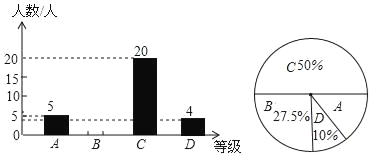
快捷英语周周练系列答案【题目】中央电视台的《朗读者》节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数量少的有![]() 本,最多的有
本,最多的有![]() 本,并根据调查结果绘制了不完整的图表,如下所示:
本,并根据调查结果绘制了不完整的图表,如下所示:
本数(本) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|

(![]() )统计图表中的
)统计图表中的![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(![]() )请将频数分布直方图补充完整.
)请将频数分布直方图补充完整.
(![]() )求所有被调查学生课外阅读的平均本数.
)求所有被调查学生课外阅读的平均本数.
(![]() )若该校八年级共有
)若该校八年级共有![]() 名学生,请你估计该校八年级学生课外阅读
名学生,请你估计该校八年级学生课外阅读![]() 本及以上的人数.
本及以上的人数.