题目内容
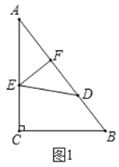
【题目】已知∠AOC与∠BOD具有公共顶点,∠COD是两个角叠合的部分.
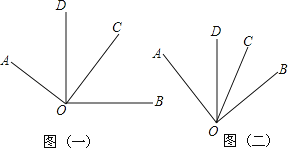
(1)若∠AOC=∠BOD=90°,观察图形(一)并完成下列问题:
①直接写出图中两个相等的锐角: = ;
②如果∠COD=40°,则∠AOB= ,若∠AOB=150°,则∠COD= ;
③猜想∠AOB+∠DOC= °,请说明理由.
(2)探究图形(二):若∠AOC=60°,∠BOD=50°,则∠AOB+∠DOC= °,请说明理由.
【答案】(1)①∠AOD,∠BOC;②140°,30°;③180°,理由见解析;(2)110°,理由见解析
【解析】
(1)①利用同角的余角相等得出答案即可;
②③利用余角的意义和角的和差计算即可;
(2)利用角的和与差计算即可.
解:(1)①若∠AOC=∠BOD=90°,
∠AOD+∠COD=∠BOC+∠COD=90°,
∴∠AOD=∠BOC;
②∵∠COD=40°,
∴∠AOD=50°,
∠AOB=∠AOD+∠BOD=140°;
若∠AOB=150°,则∠AOD=∠AOB﹣90°=60°,
∴∠COD=90°﹣∠AOD=30°.
③∠AOB+∠DOC=180°,
理由:∠AOB+∠DOC=90°+∠AOD+∠DOC=90°+90°=180°;
(2)∠AOB+∠DOC=110°,
理由:若∠AOC=60°,∠BOD=50°,
则∠AOB+∠DOC=∠AOD+∠DOC+∠BOC+∠DOC=∠AOC+∠BOD=110°.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目