题目内容
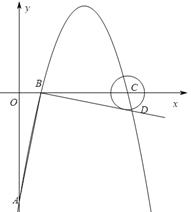
如图,已知抛物线 的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。

(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标。
 的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标。
解:(1)设直线BC的解析式为 ,
,
将B(5,0),C(0,5)代入,得 ,得
,得 。
。
∴直线BC的解析式为 。
。
将B(5,0),C(0,5)代入 ,得
,得 ,得
,得 。
。
∴抛物线的解析式 。
。
(2)∵点M是抛物线在x轴下方图象上的动点,∴设M 。
。
∵点N是直线BC上与点M横坐标相同的点,∴N 。
。
∵当点M在抛物线在x轴下方时,N的纵坐标总大于M的纵坐标。
∴ 。
。
∴MN的最大值是 。
。
(3)当MN取得最大值时,N 。
。
∵ 的对称轴是
的对称轴是 ,B(5,0),∴A(1,0)。∴AB=4。
,B(5,0),∴A(1,0)。∴AB=4。
∴ 。
。
由勾股定理可得, 。
。
设BC与PQ的距离为h,则由S1=6S2得: ,即
,即 。
。
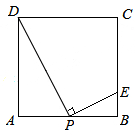
如图,过点B作平行四边形CBPQ的高BH,过点H作x轴的垂线交点E ,则BH= ,EH是直线BC沿y轴方向平移的距离。
,EH是直线BC沿y轴方向平移的距离。

易得,△BEH是等腰直角三角形,
∴EH= 。
。
∴直线BC沿y轴方向平移6个单位得PQ的解析式:
 或
或 。
。
当 时,与
时,与 联立,得
联立,得
 ,解得
,解得 或
或 。此时,点P的坐标为(-1,12)或(6,5)。
。此时,点P的坐标为(-1,12)或(6,5)。
当 时,与
时,与 联立,得
联立,得
 ,解得
,解得 或
或 。此时,点P的坐标为(2,-3)或(3,-4)。
。此时,点P的坐标为(2,-3)或(3,-4)。
综上所述,点P的坐标为(-1,12)或(6,5)或(2,-3)或(3,-4)。
 ,
,将B(5,0),C(0,5)代入,得
 ,得
,得 。
。∴直线BC的解析式为
 。
。将B(5,0),C(0,5)代入
 ,得
,得 ,得
,得 。
。∴抛物线的解析式
 。
。(2)∵点M是抛物线在x轴下方图象上的动点,∴设M
 。
。∵点N是直线BC上与点M横坐标相同的点,∴N
 。
。∵当点M在抛物线在x轴下方时,N的纵坐标总大于M的纵坐标。
∴
 。
。∴MN的最大值是
 。
。(3)当MN取得最大值时,N
 。
。∵
 的对称轴是
的对称轴是 ,B(5,0),∴A(1,0)。∴AB=4。
,B(5,0),∴A(1,0)。∴AB=4。∴
 。
。由勾股定理可得,
 。
。设BC与PQ的距离为h,则由S1=6S2得:
 ,即
,即 。
。如图,过点B作平行四边形CBPQ的高BH,过点H作x轴的垂线交点E ,则BH=
 ,EH是直线BC沿y轴方向平移的距离。
,EH是直线BC沿y轴方向平移的距离。
易得,△BEH是等腰直角三角形,
∴EH=
 。
。∴直线BC沿y轴方向平移6个单位得PQ的解析式:
 或
或 。
。当
 时,与
时,与 联立,得
联立,得 ,解得
,解得 或
或 。此时,点P的坐标为(-1,12)或(6,5)。
。此时,点P的坐标为(-1,12)或(6,5)。当
 时,与
时,与 联立,得
联立,得 ,解得
,解得 或
或 。此时,点P的坐标为(2,-3)或(3,-4)。
。此时,点P的坐标为(2,-3)或(3,-4)。综上所述,点P的坐标为(-1,12)或(6,5)或(2,-3)或(3,-4)。
(1)由B(5,0),C(0,5),应用待定系数法即可求直线BC与抛物线的解析式。
(2)构造MN关于点M横坐标的函数关系式,应用二次函数最值原理求解。
(3)根据S1=6S2求得BC与PQ的距离h,从而求得PQ由BC平移的距离,根据平移的性质求得PQ的解析式,与抛物线 联立,即可求得点P的坐标。
联立,即可求得点P的坐标。
(2)构造MN关于点M横坐标的函数关系式,应用二次函数最值原理求解。
(3)根据S1=6S2求得BC与PQ的距离h,从而求得PQ由BC平移的距离,根据平移的性质求得PQ的解析式,与抛物线
 联立,即可求得点P的坐标。
联立,即可求得点P的坐标。
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 的顶点坐标是( ).
的顶点坐标是( ).
 向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为【 】
向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为【 】