Question

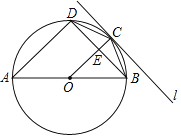
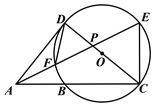
【题目】如图，△ACE，△ACD均为直角三角形，∠ACE=90°，∠ADC=90°，AE与CD相交于点P，以CD为直径的⊙O恰好经过点E，并与AC，AE分别交于点B和点F．

（1）求证：∠ADF=∠EAC．

（2）若PC=PA，PF=1，求AF的长．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

(1)由∠ACE=90°，得到∠EAC+∠FEC=90°．由∠ADC=90°，得到∠ADF+∠CDF=90°．从而有∠ADF=∠EAC;

(2)连接FC．先证△CPF∽△APC，再由相似三角形的性质得到PA的长，从而得到结论．

(1)证明：∵∠ACE=90°，

∴∠EAC+∠FEC=90°．

∵∠ADC=90°，

∴∠ADF+∠CDF=90°．

又∵∠CDF=∠FEC，

∴∠ADF=∠EAC．

(2)如图，连接FC．

∵CD为⊙O的直径，

∴∠CFD=90°，

∴∠PCF+∠CDF=90°．

∵∠CDF=∠AEC，

∴∠CDF=∠PAC．

又∵∠CPF=∠APC，

∴△CPF∽△APC，

∴，

∵PC=PA，PF=1，

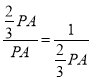∴，解得：PA=，

∴AF=PA-PF=-1=．