题目内容
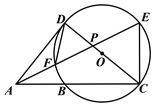
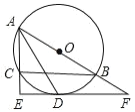
【题目】如图, O 是 ABC 的外接圆,AB 为直径,∠BAC 的平分线交O 于点 D,过点 D 作 DE⊥AC 分别交 AC、AB 的延长线于点 E、F.
(1)求证:EF 是O 的切线;
(2)若 AC=6,CE=3,求弧BD 的长度.(结果保留π)
【答案】(1)证明见解析;(2)2π.
【解析】
(1)证明切线可以连切点,作半径,即连接![]() ,利用等腰三角形
,利用等腰三角形![]() 以及
以及![]() 的角平分线证明
的角平分线证明![]() ,从而得到
,从而得到![]() ,便可证出EF 是O 的切线;
,便可证出EF 是O 的切线;
(2)过![]() 作
作![]() ,连接
,连接![]() ,根据直径所对的圆周角为直角得到
,根据直径所对的圆周角为直角得到![]() 为直角三角形,四边形
为直角三角形,四边形![]() 为矩形,且
为矩形,且![]() 为
为![]() 的中点,可以得到
的中点,可以得到![]() ,那么半径就为6,再根据
,那么半径就为6,再根据![]() 的角平分线可以得到
的角平分线可以得到![]() ,从而得到
,从而得到![]() ,求出
,求出![]() ,在
,在![]() 中,根据勾股定理求出
中,根据勾股定理求出![]() ,发现
,发现![]() ,所以
,所以![]() ,利用弧长公式求出弧BD 的长度.
,利用弧长公式求出弧BD 的长度.
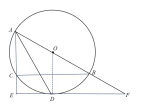
(1)连接![]()
![]()
![]()
![]()
又![]()
![]() 平分
平分![]()
![]()
![]()
![]()
又![]()
![]()
![]()
![]() EF 是O 的切线;
EF 是O 的切线;
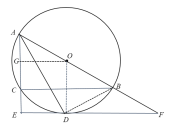
(2)过![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,如下图所示:
,如下图所示:
![]()
![]() 四边形
四边形![]() 是矩形
是矩形
又![]()
![]() 为
为![]() 的中点
的中点
![]()
![]()
![]()
![]() 平分
平分![]()
![]()
又![]()
![]() 是
是![]() 的直径
的直径
![]()
![]()
![]()
![]()
![]()
![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
![]()
![]() 的长度为:
的长度为:![]() ;
;

练习册系列答案
相关题目