题目内容
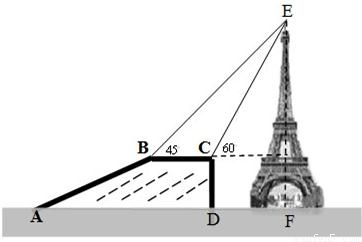
如图,已知D是BC延长线上一点,DE切△ABC的外接圆于E,DE∥AC,AE、BC的延长线交于G,BE交AC于F.(1)求证:AE2=AB•CD;
(2)若AE=2,EG=6,AB=3,求GD的长.

【答案】分析:(1)首先连接EC,由弦切角定理,易证得∠DEC=∠EAC,又由DE∥AC,易证得∠DEC=∠ACE,即可得∠ACE=∠EAC,由等角对等边即可证得AE=EC,易证得△BEA∽△EDC,然后由相似三角形的对应边成比例,即可证得结论;
(2)由(1)可求得CD的长,然后根据平行线分线段成比例定理,即可求得GD的长.
解答:(1)证明:连接EC,
∵DE切△ABC的外接圆于E,
∴∠DEC=∠EAC,
∵DE∥AC,
 ∴∠ACE=∠DEC,
∴∠ACE=∠DEC,
∴∠ACE=∠EAC,
∴AE=CE,
∵∠ABE=∠ACE,
∴∠ABE=∠DEC,
∵∠ECD+∠BCE=180°,∠BAE+∠BCE=180°,
∴∠BAE=∠ECD,
∴△BEA∽△EDC,
∴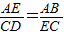 ,
,
∴AE•EC=AB•CD,
∴AE2=AB•CD;
(2)解:∵AE=2,AB=3,
∴CD= =
= ,
,
∵DE∥AC,EG=6,
∴ ,
,
即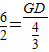 ,
,
解得:GD=4.
点评:此题考查了弦切角定理、等腰三角形的判定与性质、相似三角形的判定与性质以及平行线分线段成比例定理.此题难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.
(2)由(1)可求得CD的长,然后根据平行线分线段成比例定理,即可求得GD的长.
解答:(1)证明:连接EC,
∵DE切△ABC的外接圆于E,
∴∠DEC=∠EAC,
∵DE∥AC,
 ∴∠ACE=∠DEC,
∴∠ACE=∠DEC,∴∠ACE=∠EAC,
∴AE=CE,
∵∠ABE=∠ACE,
∴∠ABE=∠DEC,
∵∠ECD+∠BCE=180°,∠BAE+∠BCE=180°,
∴∠BAE=∠ECD,
∴△BEA∽△EDC,
∴
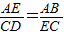 ,
,∴AE•EC=AB•CD,
∴AE2=AB•CD;
(2)解:∵AE=2,AB=3,
∴CD=
 =
= ,
,∵DE∥AC,EG=6,
∴
 ,
,即
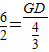 ,
,解得:GD=4.
点评:此题考查了弦切角定理、等腰三角形的判定与性质、相似三角形的判定与性质以及平行线分线段成比例定理.此题难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
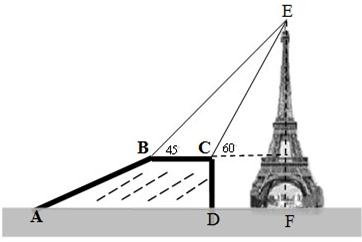
 .根据上述测量数据能否求出塔高?若能,请求出塔高(精确到1米);若不能,说明还需测出哪些量才能求出塔高.
.根据上述测量数据能否求出塔高?若能,请求出塔高(精确到1米);若不能,说明还需测出哪些量才能求出塔高.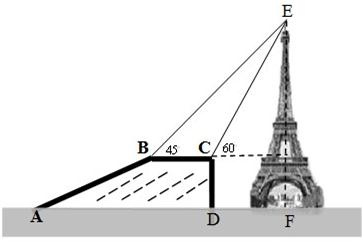
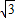 .根据上述测量数据能否求出塔高?若能,请求出塔高(精确到1米);若不能,说明还需测出哪些量才能求出塔高.
.根据上述测量数据能否求出塔高?若能,请求出塔高(精确到1米);若不能,说明还需测出哪些量才能求出塔高.