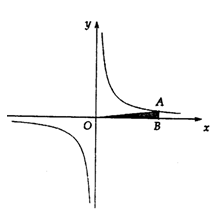
题目内容
 如图,已知点A在反比例函数y=
如图,已知点A在反比例函数y=| 4 |
| x |
| k |
| x |
AB∥x轴,分别过点A、B作x轴作垂线,垂足分别为C、D,若OC=
| 1 |
| 3 |
12
12
.分析:首先设A(a,b),再根据点A在反比例函数y=
的图象上可得ab=4,然后表示出B点坐标,再根据点B在反比例函数y=
(k≠0)的图象上可得k的值.
| 4 |
| x |
| k |
| x |
解答:解:设A(a,b),
∵点A在反比例函数y=
的图象上,
∴ab=4,
∵OC=a,OC=
OD,
∴OD=3a,
∴B(3a,b),
∵点B在反比例函数y=
(k≠0)的图象上,
∴k=3ab=3×4=12,
故答案为:12.
∵点A在反比例函数y=
| 4 |
| x |
∴ab=4,
∵OC=a,OC=
| 1 |
| 3 |
∴OD=3a,
∴B(3a,b),
∵点B在反比例函数y=
| k |
| x |
∴k=3ab=3×4=12,
故答案为:12.
点评:此题主要考查了反比例函数综合题,关键是掌握凡是反比例函数图象经过的点,横纵坐标之积=k.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


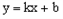 的图象与反比例函数
的图象与反比例函数 的图象相交于A、B两点。
的图象相交于A、B两点。 在一次函数的图象上,点
在一次函数的图象上,点 在反比函数的图象上。当
在反比函数的图象上。当 时,直接写出m的取值范围。
时,直接写出m的取值范围。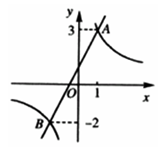
 的图象相交于A、B两点。
的图象相交于A、B两点。
 的图象经过点A(3,m),过点A作
的图象经过点A(3,m),过点A作 轴于点B,
轴于点B, 的面积为
的面积为
 的图象上,求当
的图象上,求当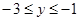 时,对应的x的取值范围;
时,对应的x的取值范围;